河北省唐山市路北区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 将方程（x﹣1）²＝6化成一元二次方程的一般形式，正确的是（）

A、x²﹣2x+5＝0 B、x²﹣2x﹣5＝0 C、x²+2x﹣5＝0 D、x²+2x+5＝0

查看试题解析
2. 下列关系式中，属于二次函数（ $x$ 为自变量）的是（）

A、 $y = π x^{2}$ B、 $y = 2 x$ C、 $y = \frac{1}{x}$ D、y=-x+1

查看试题解析
3. 抛物线y＝ ${(x - 2)}^{2} + 3$ 的顶点是（）

A、(2,-3) B、(1,4) C、(3,4) D、(2,3)

查看试题解析
4. 如图， $A B$ 为 $⊙ O$ 的弦，半径 $O C$ 交 $A B$ 于点 $D$ ， $A D = D B$ ， $O C = 5$ ， $O D = 3$ ，则 $A B$ 的长为（）

A、8 B、6 C、4 D、2

查看试题解析
5. 下列一元二次方程有两个相等的实数根的是（）

A、x²+2x=0 B、（x﹣1）²=0 C、x²=1 D、x²+1=0

查看试题解析
6. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A、y=﹣2（x﹣1）²+2 B、y=﹣2（x﹣1）²﹣2 C、y=﹣2（x+1）²+2 D、y=﹣2（x+1）²﹣2

查看试题解析
7. 用配方法解一元二次方程x²﹣6x﹣4=0，下列变形正确的是（）

A、（x﹣6）²=﹣4+36 B、（x﹣6）²=4+36 C、（x﹣3）²=﹣4+9 D、（x﹣3）²=4+9

查看试题解析
8. 关于二次函数 $y = x^{2} - 4 x - 4$ 的说法，正确的是（）

A、最大值为-4 B、最小值为-4 C、最大值为-8 D、最小值为-8

查看试题解析
9. 如图，⊙O的直径AB＝8，点C在⊙O上，∠ABC＝30°，则AC的长是（）

A、2 B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ D、4

查看试题解析
10. 如图，A、B、C是⊙O上的三点，且∠ABC=70°，则∠AOC的度数是（）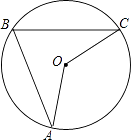

A、35° B、140° C、70° D、70°或 140°

查看试题解析
11. 某商品原价800元，连续两次降价a％后售价为578元，下列所列方程正确的是（）

A、800（1+a%）²=578 B、800（1－a%）²=578 C、800（1－2a%）=578 D、800（1－a²%）=578

查看试题解析
12. 如图为二次函数 $y = a x^{2} + b x + c$ 的图象，且此图象过 $A (- 1 ， 1)$ 、 $B (2 ， - 1)$ 两点．则结论正确的是（）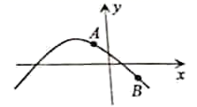

A、 $y$ 的最大值小于0 B、当 $x = 3$ 时， $y$ 的值小于0 C、当 $x = 1$ 时， $y$ 的值大于1 D、当 $x = 0$ 时， $y$ 的值大于1

查看试题解析
13. 如下图：⊙O的直径为10，弦AB的长为8，点P是弦AB上的一个动点，使线段OP的长度为整数的点P有（）

A、3 个 B、4个 C、5个 D、6个

查看试题解析
14. 当a﹣1≤x≤a时，函数y＝x²﹣2x+1的最小值为1，则a的值为（）

A、1 B、2 C、1或2 D、0或3

查看试题解析

二、填空题

15. 若关于x的一元二次方程（m﹣2）x²+x+m²﹣4＝0的一个根为0，则m值是．

查看试题解析
16. 抛物线 $y = - x^{2} + b x + c$ 的部分图象如图所示，则关于x的一元二次方程 $- x^{2} + b x + c = 0$ 的解为．

查看试题解析
17. 在 $Δ A B C$ 中， $∠ A = 40 °$ ， $⊙ O$ 截 $Δ A B C$ 三边所得的线段相等，那么 $∠ B O C$ 的度数是．

查看试题解析
18. 若二次函数y＝x²+2x+m的图象与坐标轴有3个交点，则m的取值范围是.

查看试题解析

三、解答题

19. 解方程：

(1)、 $2 x^{2} + 3 x - 1 = 0$ ；

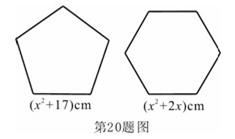
(2)、 ${(2 x + 3)}^{2} = 4 (2 x + 3)$ ．

查看试题解析
20. 抛物线顶点坐标是 $(2, - 1)$ 且经过点 $C (5, 8)$ ．

(1)、求该抛物线的解析式；

(2)、求该抛物线与坐标轴的交点坐标．

查看试题解析
21. 关于x的一元二次方程x²+（m+4）x﹣2m﹣12＝0，求证：

(1)、方程总有两个实数根；

(2)、如果方程的两根相等，求此时方程的根.

查看试题解析
22. 如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为( $x^{2} + 17$ ) $c m$ ，正六边形的边长为( $x^{2} + 2 x$ )cm（其中 $x > 0$ )，求这两段铁丝的总长

查看试题解析
23. 如图，已知二次函数y＝x²+ax+3的图象经过P点（2，3）.

(1)、求a的值和图象的顶点坐标.

(2)、点Q（m，n）在该二次函数的图象上.
①当m＝﹣2时，求n的值；

②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围.

查看试题解析
24. 如图， $A B$ 是 $⊙ O$ 的直径， $A M$ 和 $B N$ 是它的两条切线， $D E$ 切 $⊙ O$ 于点 $E$ ，交 $A M$ 于点 $D$ ，交 $B N$ 于点 $C$ ， $F$ 是 $C D$ 的中点，连接 $O F$ ．

(1)、求证： $O D / / B E$ ；

(2)、猜想： $O F$ 与 $C D$ 有何数量关系？并说明理由．

查看试题解析
25. 如图，AB ， AC是⊙O的两条弦，且 $\overset{⌢}{AB} = \overset{⌢}{AC}$ ．

(1)、求证：AO平分∠BAC；

(2)、若AB＝4 $\sqrt{5}$ ，BC＝8，求半径OA的长．

查看试题解析
26. 已知抛物线 $y = a (x - 1) (x - 3) (a \neq 0)$ 与 $y$ 轴交于点 $C$ ，且 $O C = 3$ ．

(1)、求抛物线的解析式及顶点 $D$ 的坐标；

(2)、若 $M (x_{1} ， y_{1})$ ， $N (5 ， y_{2})$ 均在该抛物线上，且 $y_{1} < y_{2}$ ，求 $M$ 点横坐标 $x_{1}$ 的取值范围；

(3)、点 $P$ 为抛物线在直线 $B C$ 下方图象上的一动点，当 $Δ P B C$ 面积最大时，求点 $P$ 的坐标．

查看试题解析