河北省石家庄市正定县2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 为筹备班级联欢会,班长对全班同学爱吃哪几种水果做了民意调查,然后决定买什么水果,最值得关注的应该是统计调查数据的( )A、中位数 B、平均数 C、众数 D、方差2. 下列方程中,一定是关于 的一元二次方程的是( )A、 B、 C、 D、3. 已知线段a=4,b=16,线段c是线段a , b的比例中项,那么线段c的长为( )A、10 B、8 C、-8 D、±84. 数据 , ,0,1,2的方差是( )A、0 B、 C、2 D、45. 如图,是一个简单的数值运算程序,则输入x的值为( )
 A、 B、 C、 或 D、无法确定6. 用配方法解一元二次方程
A、 B、 C、 或 D、无法确定6. 用配方法解一元二次方程 时,原方程可变形为( ) A、 B、 C、 D、7. 如图,在 中, , , , ,则 的长为( )
时,原方程可变形为( ) A、 B、 C、 D、7. 如图,在 中, , , , ,则 的长为( ) A、1 B、2 C、4 D、68. 如图,河堤横断面迎水坡AB的坡比是 ,堤高BC=10m,则坡面AB的长度是( )
A、1 B、2 C、4 D、68. 如图,河堤横断面迎水坡AB的坡比是 ,堤高BC=10m,则坡面AB的长度是( ) A、15m B、 C、20m D、9. 关于x的一元二次方程kx2+2x+1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k≥﹣1 C、k≠0 D、k<1且k≠010. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )
A、15m B、 C、20m D、9. 关于x的一元二次方程kx2+2x+1=0有两个不相等的实数根,则k的取值范围是( )A、k>﹣1 B、k≥﹣1 C、k≠0 D、k<1且k≠010. 如图,点A为∠α边上的任意一点,作AC⊥BC于点C,CD⊥AB于点D,下列用线段比表示cosα的值,错误的是( )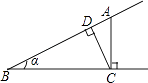 A、 B、 C、 D、11. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
A、 B、 C、 D、11. 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( ) A、1:3 B、1:4 C、1:5 D、1:2512. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)2=182 B、50+50(1+x)+50(1+x)2=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)=18213. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( )
A、1:3 B、1:4 C、1:5 D、1:2512. 某农机厂四月份生产零件50万个,第二季度共生产零件182万个.设该厂五、六月份平均每月的增长率为x,那么x满足的方程是( )A、50(1+x)2=182 B、50+50(1+x)+50(1+x)2=182 C、50(1+2x)=182 D、50+50(1+x)+50(1+2x)=18213. 如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为( ) A、20海里 B、10 海里 C、20 海里 D、30海里14. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )
A、20海里 B、10 海里 C、20 海里 D、30海里14. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )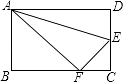 A、 B、 C、 D、15. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、 C、 D、15. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处16. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300 , 同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )
A、①处 B、②处 C、③处 D、④处16. 小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300 , 同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为( )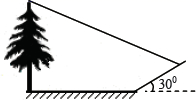 A、 米 B、12米 C、 米 D、10米
A、 米 B、12米 C、 米 D、10米二、填空题
-
17. 已知 ,则 的值为18. 计算: .19. 如图,有-块形状为 的斜板余料.已知 , , ,要把它加工成一个形状为 的工件,使 在 上, , 两点分别在 , 上,且 ,则 的面积为 .
 20. 如图所示,在 中, , , ,点 从 开始沿 边向点 以 的速度移动;点 从 开始沿 边向点 以 的速度移动,如果 , 同时出发,用 表示时间 ,那么当x=s时,以 , , 为顶点的三角形与 相似.
20. 如图所示,在 中, , , ,点 从 开始沿 边向点 以 的速度移动;点 从 开始沿 边向点 以 的速度移动,如果 , 同时出发,用 表示时间 ,那么当x=s时,以 , , 为顶点的三角形与 相似.
三、解答题
-
21. 解方程:(1)、 ;(2)、22. 某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型, :4棵; :5棵; :6棵; :7棵.将各类的人数绘制成扇形统计图和条形统计图(如图所示),经确认扇形统计图是正确的,而条形统计图尚有一处错误.

回答下列问题:
(1)、写出条形统计图中存在的不符合题意,并说明理由;(2)、写出这20名学生每人植树量的众数、中位数;(3)、在求这20名学生每人植树量的平均数时,小宇是这样分析的:第一步:求平均数的公式是 ;
第二步:在该问题中, , , , , ;
第三步: (棵).
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估这260名学生共植树多少棵.
23. 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.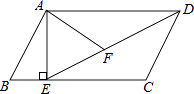 (1)、求证:△ADF∽△DEC;
(1)、求证:△ADF∽△DEC;
(2)、若AB=8,AD=6 ,AF=4 ,求AE的长.
24. 一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?