河北省石家庄市晋州市2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中是关于 $x$ 的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、 $a x^{2} + b x + c = 0$ C、 $(x - 1) (x + 2) = 1$ D、 $3 x^{2} - 2 x y - 5 y^{2} = 0$

查看试题解析
2. 方程 $x^{2} = 3 x$ 的根是（）

A、 $x = 3$ B、 $x = 0$ C、 $x_{1} = - 3 ， x_{2} = 0$ D、 $x_{1} = 3 ， x_{2} = 0$

查看试题解析
3.
如图，在平行四边形ABCD中，E为AD的中点，△BCF的面积为4，则△DEF的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 在△ABC中，∠C=90°，sinA= $\frac{\sqrt{3}}{2}$ ，则cosB的值为( )

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{1}{2}$

查看试题解析
5. 将一张矩形纸片 $A B C D$ （如图）那样折起，使顶点 $C$ 落在 $C^{'}$ 处，测量得 $A B = 4$ ， $D E = 8$ ．则 $sin ∠ C^{'} E D$ 为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
6. 把方程 $x^{2} - 4 x - 6 = 0$ 配方成 ${(x + m)}^{2} = n$ 的形式，结果应是（）

A、 ${(x - 4)}^{2} = 2$ B、 ${(x - 2)}^{2} = 6$ C、 ${(x - 2)}^{2} = 8$ D、 ${(x - 2)}^{2} = 10$

查看试题解析
7. 如图，点F是▱ABCD的边CD上一点，直线BF交AD的延长线于点E ，则下列结论错误的是（）

A、 $\frac{E D}{E A} = \frac{E F}{E B}$ B、 $\frac{E D}{D A} = \frac{D F}{C F}$ C、 $\frac{E D}{E F} = \frac{B C}{C F}$ D、 $\frac{D F}{A B} = \frac{E F}{B E}$

查看试题解析
8. 若数据2，x，4，8的平均数是4，则这组数据的中位数和众数是（　　）

A、2和3 B、3和2 C、2和2 D、2和4

查看试题解析
9. 一组数据2，3，2，3，5的方差是（）

A、6 B、3 C、1.2 D、2

查看试题解析
10. 关于x的方程mx²﹣4x﹣m+5=0，有以下说法：
①当m=0时，方程只有一个实数根；②当m=1时，方程有两个相等的实数根；③当m=﹣1时，方程没有实数根．则其中正确的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
11. 若方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 中， $a, b, c$ 满足 $4 a + 2 b + c = 0$ 和 $4 a - 2 b + c = 0$ ，则方程的根是（）

A、 $1, 0$ B、 $- 1, 0$ C、 $1, - 1$ D、 $2, - 2$

查看试题解析
12. 如图所示，在△ABC中D为AC边上一点，若∠DBC=∠A ， BC=3，AC=6，则CD的长为（）

A、1 B、2 C、 $\frac{3}{2}$ D、 $\frac{5}{2}$

查看试题解析
13. 某校规定学生的学期学业成绩由三部分组成：平时成绩占20%期中成绩占30%期末成绩占50%小颖的平时、期中、期末成绩分别为85分、90分、92分，则她本学期的学业成绩为（）

A、85 B、90 C、92 D、89

查看试题解析
14. 如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB＝5，BG＝3，则△GFH的面积为（）

A、10 B、11 C、 $\frac{15}{2}$ D、 $\frac{45}{4}$

查看试题解析
15. 如图，以 $O$ 为圆心，任意长为半径画弧，与射线 $O A$ 交于点 $B$ ，再以 $B$ 为圆心， $B O$ 长为半径画弧，两弧交于点 $C ，$ 画射线 $O C$ ，则 $t a n ∠ A O C$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
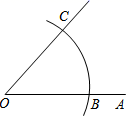16. 如图， $\frac{A E}{A F} = \frac{A B}{A C}$ ，∠1＝∠2，则对于结论： ①△ABE∽△ACF； ②△ABC∽△AEF ③ $\frac{S_{Δ A E F}}{S_{Δ A B C}} = \frac{S_{Δ A B E}}{S_{Δ A C F}}$ ④ $\frac{E F}{B C} = \frac{B E}{F C}$ ，其中正确的结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

17. 把一元二次方程3x（x﹣2）=4化为一般形式是．

查看试题解析
18. 如图，在▱ABCD的对角线BD上取一点E ．使得BE＝ $\frac{1}{4}$ BD ，延长AE交BC于G ，交DC的延长线于F ，则S_△_CFG：S_△_BEG的值为．

查看试题解析
19. 如图，矩形 $A B C D$ 的对角线 $A C$ 与 $B D$ 交于点 $O$ ，过点 $O$ 作 $B D$ 的垂线分别交 $A D ， B C$ 于 $E ， F$ 两点．若 $A C = 2 \sqrt{3} ， ∠ A E O = 120 °$ ，则 $F C$ 的长度为， $S_{△ A O E}$ 等于．

查看试题解析

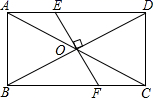
三、解答题

20. 定义新运算“ $\oplus$ ”如下：当 $a \geq b$ 时， $a \oplus b = a b + b$ ；当 $a < b$ 时， $a \oplus b = a b - a$ ，解方程 $(2 x - 1) \oplus (x + 2) = 0$

查看试题解析
21. 如图，△ABC在方格纸中．

(1)、请建立平面直角坐标系．使A、C两点的坐标分别为(2，3)、C(5，2)，求点B的坐标．

(2)、以原点O为位似中心，相似比为2，在第一象限内将△ABC放大，画出放大后的图形△A′B′C′.

(3)、计算△A′B′C′的面积S.

查看试题解析
22. 如图，在数学活动课上，小丽为了测量校园内旗杆AB的高度，站在教学楼的C处测得旗杆底端B的俯角为45°，测得旗杆顶端A的仰角为30°．已知旗杆与教学楼的距离BD=9m，请你帮她求出旗杆的高度（结果保留根号）．

查看试题解析
23. 体育课上，老师为了解女学生定点投篮的情况，随机抽取8名女生进行每人4次定点投篮的测试，进球数的统计如图所示．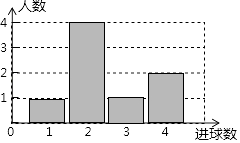

(1)、求女生进球数的平均数、中位数；

(2)、投球4次，进球3个以上（含3个）为优秀，全校有女生1200人，估计为“优秀”等级的女生约为多少人？

查看试题解析
24. 如图，在△ABC中，∠ACB＝90°，点D ， E分别是边BC ， AB上的点，且 $\frac{B E}{B A} = \frac{B D}{B C} = \frac{1}{3}$ ，连接DE并延长至点F ，使EF＝3DE ，连接CE、AF ．证明：AF＝CE ．

查看试题解析
25. 某烘焙店生产的蛋糕礼盒分为六个档次，第一档次(即最低档次)的产品每天生产76件，每件利润为10元．调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元．

(1)、若生产的某批次蛋糕每件利润为14元，此批次蛋糕属于第几档次产品？

(2)、由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？

查看试题解析
26. 如图，已知△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发(点P不与点A、B重合，点Q不与点B、C重合)，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为ts，则当t为何值时，△PBQ是直角三角形？

查看试题解析