河北省石家庄市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、填空题
-
1. 已知 ,则 .2. 如图,添加一个条件: , 使△ADE∽△ACB,(写出一个即可)
 3. 一元二次方程 的解是 .4. 如图,在⊙O中,∠ABC=50°,则∠AOC等于
3. 一元二次方程 的解是 .4. 如图,在⊙O中,∠ABC=50°,则∠AOC等于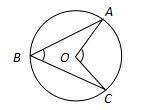 5. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .6. 如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .
5. 若关于x的一元二次方程x2+2x﹣m=0有两个相等的实数根,则m的值为 .6. 如图,已知AB为⊙O的直径,∠CAB=30°,则∠D= .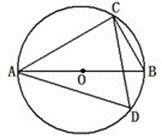 7. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3600元降到了2500元.设平均每月降价的百分率为x , 根据题意列出的方程是 .8. 如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C= .
7. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3600元降到了2500元.设平均每月降价的百分率为x , 根据题意列出的方程是 .8. 如图,AB是⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠BOE=54°,则∠C= .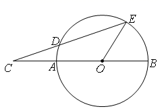 9. 如图,在四边形ABCD中,点E在AD上,EC//AB,EB//DC,若△ABE面积为5 , △ECD的面积为1,则△BCE的面积是 .
9. 如图,在四边形ABCD中,点E在AD上,EC//AB,EB//DC,若△ABE面积为5 , △ECD的面积为1,则△BCE的面积是 .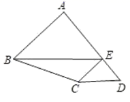 10. 关于 的方程 的解是 = , = ( 、 、 为常数, 0),则方程 的解是 .11. 如图,ED为△ABC的中位线,点G是AD和CE的交点,过点G作GF∥BC交AC于点F,如果GF=4,那么线段BC的长是 .
10. 关于 的方程 的解是 = , = ( 、 、 为常数, 0),则方程 的解是 .11. 如图,ED为△ABC的中位线,点G是AD和CE的交点,过点G作GF∥BC交AC于点F,如果GF=4,那么线段BC的长是 .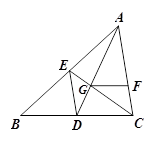 12. 如图,⊙O 的半径为3,点A是⊙O 外一点,OA=6,B是⊙O上的动点,线段AB的中点为P,连接 OA、OP.则线段 OP的最大值是 .
12. 如图,⊙O 的半径为3,点A是⊙O 外一点,OA=6,B是⊙O上的动点,线段AB的中点为P,连接 OA、OP.则线段 OP的最大值是 .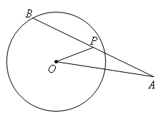
二、单选题
-
13. 一元二次方程x2﹣6x﹣5=0配方可变形为( )A、(x﹣3)2=14 B、(x﹣3)2=4 C、(x+3)2=14 D、(x+3)2=414. 如图A,B,C是 上的三个点,若 ,则 等于( )
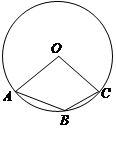 A、50° B、80° C、100° D、130°15. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与 相似的是( )
A、50° B、80° C、100° D、130°15. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与 相似的是( )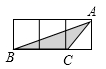 A、
A、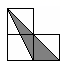 B、
B、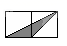 C、
C、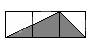 D、
D、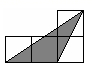 16. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )
16. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )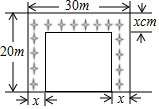 A、 B、 C、 D、17. 如图,已知⊙O的半径为3,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=4,则弦AB的长为( )
A、 B、 C、 D、17. 如图,已知⊙O的半径为3,弦AB、CD所对的圆心角分别是∠AOB、∠COD,若∠AOB与∠COD互补,弦CD=4,则弦AB的长为( )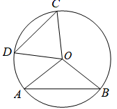 A、 B、 C、 D、18. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )
A、 B、 C、 D、18. 如图,在 中, , , .点P是边AC上一动点,过点P作 交BC于点Q,D为线段PQ的中点,当BD平分 时,AP的长度为( )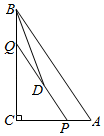 A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
19. 解下列方程:(1)、(2)、20. 已知:如图,D是AC上一点,DE∥AB,∠B=∠DAE.
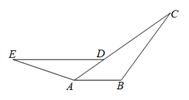 (1)、求证:△ABC∽△DAE;(2)、若AB=8,AD=6,AE=12,求BC的长.21. 如图,已知⊙O的弦AB,E,F是弧AB上两点,弧AE=弧BF,OE、OF分别交于AB于C、D两点,求证:AC=BD.
(1)、求证:△ABC∽△DAE;(2)、若AB=8,AD=6,AE=12,求BC的长.21. 如图,已知⊙O的弦AB,E,F是弧AB上两点,弧AE=弧BF,OE、OF分别交于AB于C、D两点,求证:AC=BD.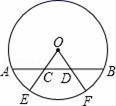 22. 已知:关于x的方程x2+2mx+m2-1=0(1)、不解方程,判别方程根的情况;(2)、若方程有一个根为3,求m的值.23. 如图,在 网格图中, 与 是位似图形.
22. 已知:关于x的方程x2+2mx+m2-1=0(1)、不解方程,判别方程根的情况;(2)、若方程有一个根为3,求m的值.23. 如图,在 网格图中, 与 是位似图形.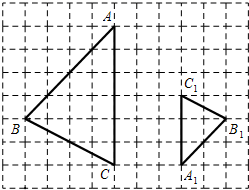 (1)、若在网格上建立平面直角坐标系,使得点A的坐标为 ,点 的坐标为 ,写出点B的坐标;(2)、以点A为位似中心,在网格图中作 ,使 和 位似,且位似比为 1:2;(3)、在图上标出 与 的位似中心P , 并写出点P的坐标,计算四边形ABCP的周长.24. 如图,在Rt△ABC中,∠ACB=90°.
(1)、若在网格上建立平面直角坐标系,使得点A的坐标为 ,点 的坐标为 ,写出点B的坐标;(2)、以点A为位似中心,在网格图中作 ,使 和 位似,且位似比为 1:2;(3)、在图上标出 与 的位似中心P , 并写出点P的坐标,计算四边形ABCP的周长.24. 如图,在Rt△ABC中,∠ACB=90°.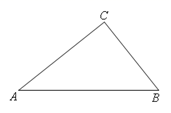 (1)、利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
(1)、利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)①作AC的垂直平分线,交AB于点O,交AC于点D;②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)、在(1)所作的图形中,解答下列问题.①判断点B与⊙O的位置关系并说明理由;②若DE=2,AC=8,求⊙O的半径.25. 山水旅行社的一则广告如下:我社组团去A风景区旅游,收费标准为:如果人数不超过30人,人均旅游费用为800元;如果人数多于30人,那么每增加1人,人均旅游费用降低10元,但人均旅游费用不得低于550元,某公司组织一批员工到A风景区旅游,支付给旅行社28000元.(1)、该公司的人数30人(填“大于、小于或等于”)(2)、求该公司的人数.26. 如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米.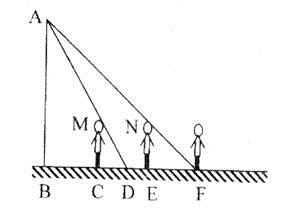 (1)、求路灯A的高度;(2)、当王华再向前走2米,到达F处时,他的影长是多少?27. 已知:在△ABC中,以AC边为直径的⊙O交BC于点D(BD > CD),在劣弧 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)、求路灯A的高度;(2)、当王华再向前走2米,到达F处时,他的影长是多少?27. 已知:在△ABC中,以AC边为直径的⊙O交BC于点D(BD > CD),在劣弧 上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.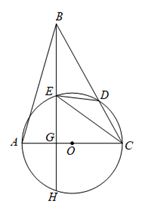 (1)、求证:AC⊥BH;(2)、若∠ABC=45°,⊙O的直径等于 ,BC=10,求CE的长.28. 在矩形ABCD中,AB=4,AD=10,E是AD上的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG、FG,FG交AD于点N.
(1)、求证:AC⊥BH;(2)、若∠ABC=45°,⊙O的直径等于 ,BC=10,求CE的长.28. 在矩形ABCD中,AB=4,AD=10,E是AD上的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG、FG,FG交AD于点N.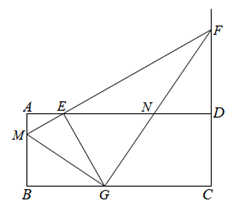 (1)、当点M为AB中点时,求DF与EG的长;(2)、在整个运动过程中, 的值是否会变化,若不变,求出它的值;若变化,请说明理由;(3)、若△EGN为等腰三角形时,请直接写出所有满足条件的AM的长度.
(1)、当点M为AB中点时,求DF与EG的长;(2)、在整个运动过程中, 的值是否会变化,若不变,求出它的值;若变化,请说明理由;(3)、若△EGN为等腰三角形时,请直接写出所有满足条件的AM的长度.