北京市丰台区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 下面四个图形分别是绿色食品、节水、节能和回收标志,在这四个标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标为( )A、 B、 C、 D、3. 将抛物线 向左平移2个单位,再向下平移3个单位得到的抛物线是( )A、 B、 ; C、 D、4. 二次函数 的图象如图所示,则下列关于该函数说法中正确的是( )
2. 抛物线 的顶点坐标为( )A、 B、 C、 D、3. 将抛物线 向左平移2个单位,再向下平移3个单位得到的抛物线是( )A、 B、 ; C、 D、4. 二次函数 的图象如图所示,则下列关于该函数说法中正确的是( ) A、 B、 C、 D、5. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为 的雷达,监测点的分布情况如图,如果将雷达装置设在 点,每一个小格的边长为 那么能被雷达监测到的最远点为( )
A、 B、 C、 D、5. 雷达通过无线电的方法发现目标并测定它们的空间位置,因此雷达被称为“无线电定位”.现有一款监测半径为 的雷达,监测点的分布情况如图,如果将雷达装置设在 点,每一个小格的边长为 那么能被雷达监测到的最远点为( ) A、 点 B、 点 C、 点 D、 点6. 如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )
A、 点 B、 点 C、 点 D、 点6. 如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为( )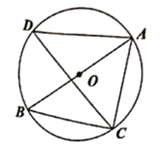 A、5 B、10 C、 D、7. 在 中, .在同一平面内,将 绕点 旋转到 ,若 恰好落在线段 上,连接 .则下列结论中错误的是( )
A、5 B、10 C、 D、7. 在 中, .在同一平面内,将 绕点 旋转到 ,若 恰好落在线段 上,连接 .则下列结论中错误的是( ) A、 B、 C、 D、8. 函数 的自变量 的取值范围为全体实数,其中 部分的图象如图所示,对于此函数有下列结论:
A、 B、 C、 D、8. 函数 的自变量 的取值范围为全体实数,其中 部分的图象如图所示,对于此函数有下列结论:
①函数图象关于 轴对称;②函数既有最大值,也有最小值;③当 时, 随 的增大而减小;④当 时,关于 的方程 有 个实数根.其中正确的结论个数是( )
A、3 B、2 C、1 D、0二、填空题
-
9. 在平面直角坐标中,点 关于原对称的点的坐标为 .10. 如图所示,四边形ABCD是圆内接四边形,其中 ,则 .
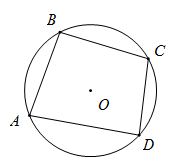 11. 写出一个二次函数,其图像满足:①开口向下;②与 轴交于点 ,这个二次函数的解析式可以是 .12. 点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转°后能与原来的图案互相重合.
11. 写出一个二次函数,其图像满足:①开口向下;②与 轴交于点 ,这个二次函数的解析式可以是 .12. 点O是正五边形ABCDE的中心,分别以各边为直径向正五边形的外部作半圆,组成了一幅美丽的图案(如图).这个图案绕点O至少旋转°后能与原来的图案互相重合.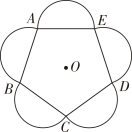 13. 如图,点P是⊙ 的直径BA的延长线上一点,PC切⊙ 于点C,若 ,PB=6,则PC等于 .
13. 如图,点P是⊙ 的直径BA的延长线上一点,PC切⊙ 于点C,若 ,PB=6,则PC等于 . 14. 若二次函数 的图象上有两点 ,mn.(填“>”,“ ”或“ ”)15. 如图,在平面直角坐标系 中,点 的坐标分别是 是 的外接圆,则圆心 的坐标为 , 的半径为 .
14. 若二次函数 的图象上有两点 ,mn.(填“>”,“ ”或“ ”)15. 如图,在平面直角坐标系 中,点 的坐标分别是 是 的外接圆,则圆心 的坐标为 , 的半径为 .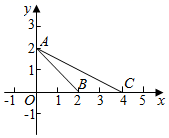
三、解答题
-
16. 在关于的 二次函数中,自变量 可以取任意实数,下表是自变量 与函数 的几组对应值:
…
1
2
3
4
5
6
7
8
…
…
-1.78
-3.70
-4.42
-3.91
-2.20
4.88
10.27
…
根据以上信息,关于 的一元二次方程 的两个实数根中,其中的一个实数根约等于(结果保留小数点后一位).
17. 已知二次函数 .(1)、用配方法将其化为 的形式;(2)、求出此二次函数的对称轴和二次函数图象与 轴交点的坐标.18. 已知一个二次函数图象上部分点的横坐标 与纵坐标 的对应值如下表所示:…
-3
-2
-1
0
1
…
…
0
3
4
3
0
…
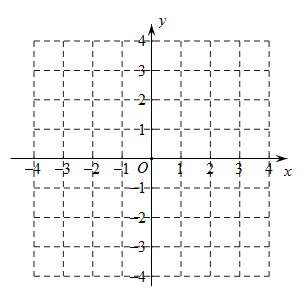 (1)、求这个二次函数的解析式;(2)、在直角坐标系中画出二次函数的图象;(3)、结合图象,直接写出当 时, 的取值范围.19. 如图, 为等边三角形,将 边绕点 顺时针旋转 ,得到线段 连接 ,求 的度数﹒
(1)、求这个二次函数的解析式;(2)、在直角坐标系中画出二次函数的图象;(3)、结合图象,直接写出当 时, 的取值范围.19. 如图, 为等边三角形,将 边绕点 顺时针旋转 ,得到线段 连接 ,求 的度数﹒ 20. 下面是“作已知三角形的高”的尺规作图过程.
20. 下面是“作已知三角形的高”的尺规作图过程.已知: .
求作: 边上的高 .
作法:如图,

①分别以点 和点 为圆心,大于 的长为半径作弧,两弧相交于 两点;
②作直线 ,交 于点 ,则直线 是线段 的 ▲ 线;
③以 为圆心, 为半径作 ,与 的延长线交于点 ,连接 ,线段 即为所作的高.
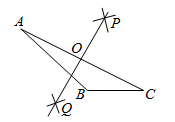 (1)、补全尺规作图并填空﹔(2)、判断 为高的依据是 .21. 如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端 分米, 为 中点, 为拱门最高点,圆心 在线段 上, 分米,求拱门所在圆的半径.
(1)、补全尺规作图并填空﹔(2)、判断 为高的依据是 .21. 如图1所示,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中拱门最下端 分米, 为 中点, 为拱门最高点,圆心 在线段 上, 分米,求拱门所在圆的半径.
 22. 如图, 的顶点坐标分别为 .
22. 如图, 的顶点坐标分别为 . (1)、请画出 关于点 成中心对称的 ,并写出点 的坐标;(2)、四边形 的面积为 .23. 已知二次函数 的图象与 轴有公共点.(1)、求 的取值范围;(2)、当 为正整数时,求此时二次函数与 轴的交点坐标.24. 如图1,单孔拱桥的形状近似抛物线形,如图2建立所示的平面直角坐标系,在正常水位时,水面宽度 为 拱桥的最高点 到水面 的距离为 .
(1)、请画出 关于点 成中心对称的 ,并写出点 的坐标;(2)、四边形 的面积为 .23. 已知二次函数 的图象与 轴有公共点.(1)、求 的取值范围;(2)、当 为正整数时,求此时二次函数与 轴的交点坐标.24. 如图1,单孔拱桥的形状近似抛物线形,如图2建立所示的平面直角坐标系,在正常水位时,水面宽度 为 拱桥的最高点 到水面 的距离为 . (1)、求抛物线的解析式;(2)、因为上游水库泄洪,水面宽度变为 ,求水面上涨的高度﹒25. 如图,AB为⊙O的直径,C,D是⊙O上的点,P是⊙O外一点,AC⊥PD于点E,AD平分∠BAC.
(1)、求抛物线的解析式;(2)、因为上游水库泄洪,水面宽度变为 ,求水面上涨的高度﹒25. 如图,AB为⊙O的直径,C,D是⊙O上的点,P是⊙O外一点,AC⊥PD于点E,AD平分∠BAC. (1)、求证:PD是⊙O的切线;(2)、若DE= ,∠BAC=60°,求⊙O的半径.26. 在平面直角坐标系 中,已知抛物线 .(1)、抛物线 的对称轴为 ;(2)、若在抛物线 上有两点 ,且 ,则 的取值范围是;(3)、若抛物线的顶点纵坐标 的取值范围为 ,求 的取值范围.27. 在学习利用旋转解决图形问题时,老师提出如下问题:(1)、如图1,点 是正方形 内一点, ,你能求出 的度数吗?
(1)、求证:PD是⊙O的切线;(2)、若DE= ,∠BAC=60°,求⊙O的半径.26. 在平面直角坐标系 中,已知抛物线 .(1)、抛物线 的对称轴为 ;(2)、若在抛物线 上有两点 ,且 ,则 的取值范围是;(3)、若抛物线的顶点纵坐标 的取值范围为 ,求 的取值范围.27. 在学习利用旋转解决图形问题时,老师提出如下问题:(1)、如图1,点 是正方形 内一点, ,你能求出 的度数吗?小明通过观察、分析、思考,形成了如下思路:

思路一:将 绕点 逆时针旋转 ,得到 ,连接 ,可求出 的度数;
思路二:将 绕点 顺时针旋转 ,得到 ,连接 ,可求出 的度数.
请参照小明的思路,任选一种写出完整的解答过程.
(2)、如图2,若点 是正方形 外一点,要使 ,线段PA,PB,PC应满足怎样的等量关系?请参考小明上述解决问题的方法进行探究,直接写出线段PA,PB,PC满足的等量关系.
 28. 对于平面上两点 ,给出如下定义:以点 或 为圆心, 长为半径的圆称为点 的“共径圆”.点 的“共径圆”的示意图如图所示.
28. 对于平面上两点 ,给出如下定义:以点 或 为圆心, 长为半径的圆称为点 的“共径圆”.点 的“共径圆”的示意图如图所示.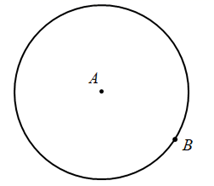

 (1)、已知点 的坐标为 ,点 的坐标为 ,则点 的“共径圆”的面积为;(2)、已知点 在以坐标原点为圆心,以 为半径的圆上,点 在直线 上,求点 的“共径圆”的半径最小值;(3)、已知点 的坐标为 ,点 是 轴及 轴上方的点,如果直线 上存在两个点 ,使得点 的“共径圆”的面积为 ,直接写出满足条件的 的取值范围.
(1)、已知点 的坐标为 ,点 的坐标为 ,则点 的“共径圆”的面积为;(2)、已知点 在以坐标原点为圆心,以 为半径的圆上,点 在直线 上,求点 的“共径圆”的半径最小值;(3)、已知点 的坐标为 ,点 是 轴及 轴上方的点,如果直线 上存在两个点 ,使得点 的“共径圆”的面积为 ,直接写出满足条件的 的取值范围.