山西省孝义市2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 下列四个选项中,不是全等图形的是( )A、
 B、
B、 C、
C、 D、
D、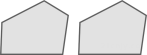 2. 以下是回收、节水、绿色包装、低碳四个标志,其中是轴对称图形的是( )A、
2. 以下是回收、节水、绿色包装、低碳四个标志,其中是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 下面四个图形中,线段 是 的高的是( )A、
3. 下面四个图形中,线段 是 的高的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图,若 , ,那么 的度数为( )
4. 如图,若 , ,那么 的度数为( ) A、 B、 C、 D、5. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )
A、 B、 C、 D、5. 如图,已知 ,那么添加下列一个条件后,仍无法判定 的是( )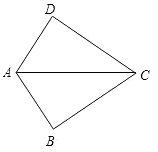 A、 B、 C、 D、6. 如图是体育场的一块三角形休息区,要在休息区内设一个供水台供大家休息饮水,要使供水台到 , , 的距离相等,供水台应该选在( )
A、 B、 C、 D、6. 如图是体育场的一块三角形休息区,要在休息区内设一个供水台供大家休息饮水,要使供水台到 , , 的距离相等,供水台应该选在( ) A、 三条角平分线的交点处 B、 三条中线的交点处 C、 三条高线所在的直线的交点处 D、 三条边的垂直平分线的交点处7. 若从一个正多边形的一个顶点出发,最多可以引5条对角线,则它的一个内角为( )A、 B、 C、 D、8. 如图, , , 分别平分 和 ,过点 分别做 于点 , 于点 ,延长 交 于点 ,若 ,则 的值为( )
A、 三条角平分线的交点处 B、 三条中线的交点处 C、 三条高线所在的直线的交点处 D、 三条边的垂直平分线的交点处7. 若从一个正多边形的一个顶点出发,最多可以引5条对角线,则它的一个内角为( )A、 B、 C、 D、8. 如图, , , 分别平分 和 ,过点 分别做 于点 , 于点 ,延长 交 于点 ,若 ,则 的值为( ) A、2 B、3 C、4 D、59. 如图,在 中, , , ,点 是三条角平分线的交点,若 的面积是 ,则 的 边上的高是( )
A、2 B、3 C、4 D、59. 如图,在 中, , , ,点 是三条角平分线的交点,若 的面积是 ,则 的 边上的高是( ) A、1 B、2 C、3 D、410. 是 的中线,点 , 分别是 和 延长线上的点,且 ,分别连接 、 ,下列说法:① ,② 和 面积相等,③ ,④ .正确的有( )
A、1 B、2 C、3 D、410. 是 的中线,点 , 分别是 和 延长线上的点,且 ,分别连接 、 ,下列说法:① ,② 和 面积相等,③ ,④ .正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,建高层建筑需要用塔吊来吊建筑材料,塔吊的上部是三角形结构,其中的数学原理是 .
 12. 如图,将一副三角板如图摆放,则图中 的度数是度.
12. 如图,将一副三角板如图摆放,则图中 的度数是度. 13. 如图, 的面积是2, 是 边上的中线, , .则 的面积为 .
13. 如图, 的面积是2, 是 边上的中线, , .则 的面积为 . 14. 如图,将长方形 沿 折叠,使点 落在 边上的点 处,若 ,则 的度数为 .
14. 如图,将长方形 沿 折叠,使点 落在 边上的点 处,若 ,则 的度数为 . 15. 如图,线段 , , 两两相交于点 , , ,分别连接 , , .则 .
15. 如图,线段 , , 两两相交于点 , , ,分别连接 , , .则 .
三、解答题
-
16. 如图,在 中, 是 边上的高, 平分 交 于点 .若 , ,求 的度数.
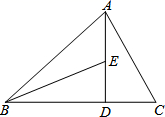 17. 如图,点 在一条直线上, , , .
17. 如图,点 在一条直线上, , , .求证: .
 18. 如图, 中, , , .
18. 如图, 中, , , . (1)、作 关于 轴对称的 ,并写出 , , 的坐标 ; ; ;(2)、作 关于直线 对称的 ,并写出 、 、 的坐标 ; ;19. 作图题.(1)、如图,已知线段 .求作 ,使得 , , .(尺规作图,不写作法,保留作图痕迹).
(1)、作 关于 轴对称的 ,并写出 , , 的坐标 ; ; ;(2)、作 关于直线 对称的 ,并写出 、 、 的坐标 ; ;19. 作图题.(1)、如图,已知线段 .求作 ,使得 , , .(尺规作图,不写作法,保留作图痕迹). (2)、①在(1)所作出的图中,作 的垂直平分线交 于点 ,交 于点 (尺规作图,不写作法,保留作图痕迹);
(2)、①在(1)所作出的图中,作 的垂直平分线交 于点 ,交 于点 (尺规作图,不写作法,保留作图痕迹);②连接 ,若 , , ,则 的周长为(直接写出答案).
20. 一位经历过战争的老战土讲述了这样一个故事:在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离,在不能过河测量又没有任何测量工具的情况下,一个战土想出来这样的办法:他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上,接着,他用步测的方法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.将这位战士看成一条线段,碉堡看成一点,示意图如下,你能根据示意图解释其中的道理吗?

下面是彤彤同学写出的不完整的已知和求证,请你补全已知和求证,并完成证明.
已知:如图, ,……….

求证:………..
证明:
21. 阅读下列材料,完成相应任务.数学活动课上,老师提出了如下问题:
如图1,已知 中, 是 边上的中线.

求证: .
智慧小组的证法如下:
证明:如图2,延长 至 ,使 ,
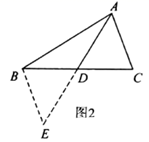
∵ 是 边上的中线∴
在 和 中
∴ (依据一)∴
在 中, (依据二)
∴ .
(1)、任务一:上述证明过程中的“依据1”和“依据2”分别是指:依据1:;
依据2: .
(2)、归纳总结:上述方法是通过延长中线 ,使 ,构造了一对全等三角形,将 , , 转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.任务二:如图3, , ,则 的取值范围是;
 (3)、任务三:如图4,在图3的基础上,分别以 和 为边作等腰直角三角形,在 中, , ; 中, , .连接 .试探究 与 的数量关系,并说明理由.
(3)、任务三:如图4,在图3的基础上,分别以 和 为边作等腰直角三角形,在 中, , ; 中, , .连接 .试探究 与 的数量关系,并说明理由. 22. 综合与实践.
22. 综合与实践.积累经验
我们在第十二章《全等三角形》中学习了全等三角形的性质和判定,在一些探究题中经常用以上知识转化角和边,进而解决问题.例如:我们在解决:“如图1,在 中, , ,线段 经过点 ,且 于点 , 于点 .求证: , ”这个问题时,只要证明 ,即可得到解决,
(1)、请写出证明过程;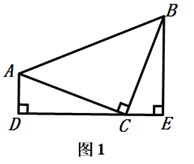 (2)、如图2,在平面直角坐标系中, 中, , ,点 的坐标为 ,点 的坐标为 ,求点 的坐标.
(2)、如图2,在平面直角坐标系中, 中, , ,点 的坐标为 ,点 的坐标为 ,求点 的坐标.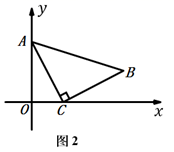 (3)、如图3, 在平面直角坐标系中, , ,点 的坐标为 ,点 的坐标为 ,则点 的坐标为 .
(3)、如图3, 在平面直角坐标系中, , ,点 的坐标为 ,点 的坐标为 ,则点 的坐标为 .