山西省朔州市右玉二中2020-2021学年八年级上学期数学期中试卷
试卷更新日期：2020-12-30 类型：期中考试
一、单选题
-
1. 下列图案属于轴对称图形的是（ ）A、
B、
C、
D、
2. 如图，已知∠1＝∠2，则下列条件中，不能使△ABC≌△DBC成立的是（ ）
A、AB＝CD B、AC＝BD C、∠A＝∠D D、∠ABC＝∠DCB3. 已知三角形的两边分别为4和10，则此三角形的第三边可能是（ ）A、4 B、5 C、9 D、144. 已知点M（3，－1）关于y轴对称的的对称点N的坐标为（a＋b，1－b），则ab的值为（ ）A、10 B、25 C、－3 D、325. 如图，一块三角形玻璃裂成①、②、③三块，现需要划一块同样大小的三角形玻璃，为了方便只需带上一块，号码和依据是（ ）
A、①SAS B、②ASA C、③AAS D、③ASA6. 如图， AD是 的中线，E、F分别是AD和AD延长线上的点，且 ，连结BF、CE ． 下列说法：①CE＝BF②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE．其中正确的有（ ）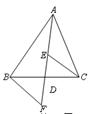
A、1个 B、2个 C、3个 D、4个7. 如图，△ABC中，∠A=60°，点E，F在AB、AC上，沿EF向内折叠△AEF，得△DEF，则图中∠1+∠2的和等于（ ）
A、 B、 C、 D、8. 不一定在三角形内部的线段是( )
A、三角形的角平分线 B、三角形的中线 C、三角形的高 D、三角形的中位线9. 如图，△ABC中，BD是 ∠ ABC的角平分线，DE ∥ BC，交AB 于 E，∠A=60°， ∠BDC=95°，则∠BED的度数是（ ）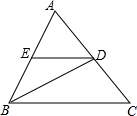
A、35° B、70° C、110° D、130°10. 如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（ ）
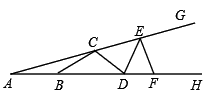A、80° B、90° C、100° D、108°二、填空题
-
11. 一个多边形的内角和与外角和的和是 ，那么这个多边形的边数n＝ ．12. 如图△ABC中，∠B＝∠C，FD⊥BC，DE⊥AB，∠AFD＝158°，则∠EDF＝.
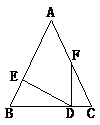13. 如图，∠1+∠2+∠3+∠4+∠5+∠6＝.
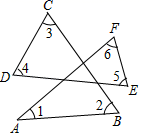14. 如图，在 中， ， ，点 的坐标为 ，点 的坐标为 ，点 的坐标是.
15. 如图在△ABC中，BF、CF是角平分线，DE∥BC，分别交AB、AC于点D、E，DE经过点F．结论：①△BDF和△CEF都是等腰三角形；②DE=BD+CE； ③△ADE的周长=AB+AC；④BF=CF．其中正确的是（填序号）
三、解答题
-
16. 计算下列各题：(1)、 ；(2)、17. 如图，已知∠C＝60°，AE，BD是 的角平分线，且交于点P．
(1)、求∠APB的度数；(2)、求证：点P在∠C的平分线上．18. 如图，小河边有两个村庄A、B．要在河边建一自来水厂向A村与B村供水．
(1)、若要使水厂到A、B村的距离相等，则应选择在哪建厂？(2)、若要使水厂到A、B村的水管最省料，应建在什么地方？（保留作图痕迹，不写作法）19. 如图，∠A＝∠D＝90°，AB＝DC，点E，F在BC上且BE＝CF．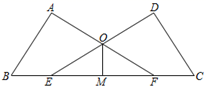
(1)、求证：AF＝DE；(2)、若OM平分∠EOF，求证：OM⊥EF．20. 如图，在平面直角坐标系中，A（3，4），B（1，2），C（5，1）．
(1)、如图中作出△ABC关于y轴的对称图形△A1B1C1；(2)、写出点A1 ， B1 ， C1的坐标（直接写答案）．A1： ， B1： ， C1：；(3)、求△ABC的面积．21. 如图，将长方形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕.
(1)、试说明：△FGC≌△EBC；(2)、若AB=8，AD=4，求四边形ECGF(阴影部分)的面积.
