山西省吕梁市交城县2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-30 类型：期中考试

进入出卷网下载

一、单选题

1. 给出下列说法：（1）等边三角形是等腰三角形；（2）三角形按边的相等关系分类可分为等腰三角形、等边三角形和不等边三角形；（3）三角形按角的大小分类可分为锐角三角形、直角三角形和钝角三角形.其中，正确的有（）个.

A、1 B、2 C、3 D、0

查看试题解析
2. 下列长度的3根小木棒不能搭成三角形的是（）

A、2cm，3cm，4cm B、1cm，2cm，3cm C、3cm，4cm，5cm D、4cm，5cm，6cm

查看试题解析
3. 下列图形中AD是三角形ABC的高线的是（）

A、 B、 C、 D、

查看试题解析
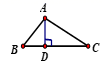4. 已知直角三角形ABC，有一个锐角等于50°，则另一个锐角的度数是（）.

A、30° B、 40° C、45° D、50°

查看试题解析
5. 如图，在△ABC中，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E，若∠A＝54°，∠B＝46°.则∠CDE的大小为（）

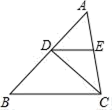A、45° B、40° C、39° D、35°

查看试题解析
6. 如图，已知AD=AE，BE=CD，∠1=∠2=100°，若∠BAE=60°，则∠CAE的度数为（）

A、40° B、60° C、80° D、100°

查看试题解析

7. 在探索多边形内角和公式的过程中，多数同学采用如下表格中分割多边形的方法，并从四边形，五边形等特殊多边形的内角和计算，得到

n

边形的内角和公式．

多边形	四边形	五边形	六边形	七边形	…	$n$ 边形
图例					…
内角和	$\begin{array}{l} (4 - 2) \times 180 ° \\ = 360 ° \end{array}$	$\begin{array}{l} (5 - 2) \times 180 ° \\ = 540 ° \end{array}$	$\begin{array}{l} (6 - 2) \times 180 ° \\ = 720 ° \end{array}$	$\begin{array}{l} (7 - 2) \times 180 ° \\ = 900 ° \end{array}$	…	$(n - 2) \times 180 °$

以上表格中：由 $(4 - 2) \times 180 ° = 360 °$ ， $(5 - 2) \times 180 ° = 540 °$ ， $(6 - 2) \times 180 ° = 720 °$ ， $(7 - 2) \times 180 ° = 900 °$ ，…，得到 $(n - 2) \times 180 °$ 的结论，体现的数学思想是：（）

A、数形结合 B、类比 C、由特殊到一般 D、公理化

查看试题解析

8. 如图，若△ABC 与△A′B′C′关于直线 MN 对称，BB′交 MN 于点 O，则下列说法不一定正确的是（）

A、AC＝A′C′ B、BO＝B′O C、AA′⊥MN D、AB∥B′C′

查看试题解析
9. 如图，MN是线段AB的垂直平分线，C在MN外，且与A点在MN的同一侧，BC交MN于P点，则（）

A、BC>PC+AP B、BC<PC+AP C、BC=PC+AP D、BC≥PC+AP

查看试题解析
10. 如图，将△ABC折叠，使点A与BC边中点D重合，折痕为MN，若AB=9，BC=6，则△DNB的周长为（）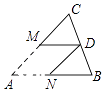

A、12 B、13 C、14 D、15

查看试题解析

二、填空题

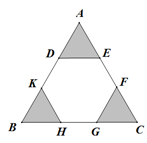
11. 如果一个多边形的内角和为1620°，那么这个多边形的一个顶点有条对角线．

查看试题解析
12. 如图，把边长为12的正三角形ABC纸板剪去三个小正三角形（阴影部分），得到正六边形DEFGHK，则剪去的小正三角形的边长为．

查看试题解析
13. 如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为.

查看试题解析
14. 如图，AB=AC，BE=CD，要使 $△ A B E ≅ △ A C D$ ，依据SSS，则还需添加条件．（填一个即可）

查看试题解析
15. 已知两点的坐标分别是（-2，3）和（2，3），给出下列说法：①两点关于 $x$ 轴对称；②两点关于 $y$ 轴对称；③两点之间的距离为4．其中正确的是．（填序号）

查看试题解析
16. 如图，AB⊥CD，且AB=CD，E，F是AD上两点，CF⊥AD，BE⊥AD．若CF=8，BE=6，AD=10，则EF的长为．

查看试题解析
17. 如图，在△ABC中，AB=AC=10，BC=12，AD=8，AD是∠BAC的平分线．若E是AC上一点且BE⊥AC，P是AD的动点，则PC+PE的最小值是．

查看试题解析
18. 已知O为等边三角形ABD的边BD的中点，AB=4，E，F分别为射线AB，DA上一动点，且∠EOF=120°，若AF=1，则BE的长为．

查看试题解析

三、解答题

19.

(1)、如图，已知△ABC，请用尺规过点A作一条直线，使其将△ABC分成面积相等的两部分．（不写已知、求作、作法，只保留作图痕迹）

(2)、如图，已知△ABC在平面直角坐标系中的位置如图所示．
①作出△ABC关于 $y$ 轴对称的 $Δ A_{1} B_{1} C_{1}$ ，并写出 $Δ A_{1} B_{1} C_{1}$ 各顶点的坐标；

②将△ABC向右平移6个单位长度，作出平移后的 $Δ A_{2} B_{2} C_{2}$ ，并写出 $Δ A_{2} B_{2} C_{2}$ 各顶点的坐标；

③观察 $Δ A_{1} B_{1} C_{1}$ 与 $Δ A_{2} B_{2} C_{2}$ ，它们是否关于某条直线对称？若是，请在图上画出这条对称轴．

查看试题解析
20. 如图，在四边形ABCD中，E是CB的中点，延长AE、DC相交于点F，∠CEA＝∠B+∠F.求证：AB＝FC.

查看试题解析
21.
如图，已知△ABC为等边三角形，D为BC延长线上的一点，CE平分∠ACD，CE=BD，求证：△ADE为等边三角形．

查看试题解析
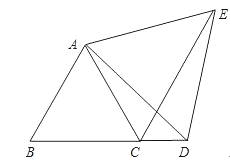22. 如图，在Rt△ABC中，∠BAC=90°，∠ABC=60°，AD，CE分别平分∠BAC，∠ACB，AD与CE交于点O，连接OB．

(1)、若OF⊥AC于点F，AB=4，OF= $2 \sqrt{3} - 2$ ．求△BOC的面积；

(2)、求证：AC=AE+CD．

查看试题解析
23. 综合探究：探索等腰三角形中相等的线段

问题情境：

数学活动课上，老师提出了一个问题：等腰三角形底边中点到两腰的距离相等吗？同学们就这个问题展开探究．

问题初探：

(1)、希望小组的同学们根据题意画出了相应的图形，如图1．在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为点E，F．经过合作，该小组的同学得出的结论是DE=DF．并且展示了他们的证法如下：
证明：如图1，

∵DE⊥AB，DF⊥AC

∴∠DEB=∠DFC=90°

∵AB=AC

∴∠B=∠C（依据1）

∵D是BC的中点

∴BD=CD

在△BDE和△CDF中

${\begin{matrix} ∠ D E B = ∠ D F C \\ ∠ B = ∠ C \\ B D = C D \end{matrix}$

∴△BDE≌△CDF（依据2）

∴DE=DF

①请写出依据1和依据2的内容

依据1：．

依据2：

②请你应用图2写出一种不同于希望小组的证法．

(2)、问题再探：
未来小组的同学经过探究又有新的发现，如果在等腰三角形ABC中，作腰AB上的高CG，如图3．则CG与DE有确定的数量关系．请你直接写出这个数量关系为．

(3)、类比探究：
奋斗小组的同学认真研究过后，发现了以下两个符合题意结论：①在图4中，若DE，DF分别为△ABD和△ACD的中线，那么DE=DF仍然成立；②在图5中，若DE，DF分别为△ABD和△ACD的角平分线，那么DE=DF仍然成立．请你选择其中一个结论，写出证明过程．

查看试题解析