山西省晋中市寿阳县2020-2021学年八年级上学期数学期中试卷
试卷更新日期:2020-12-30 类型:期中考试
一、单选题
-
1. 在下列实数中,是无理数的为( ).A、0 B、 C、 D、2. 如图,小手盖住的点的坐标可能是( ).
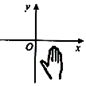 A、(5,2) B、(-6,3) C、(-4,6) D、(3,-4)3. 下列图象中,表示y是x的函数的有 ( )
A、(5,2) B、(-6,3) C、(-4,6) D、(3,-4)3. 下列图象中,表示y是x的函数的有 ( )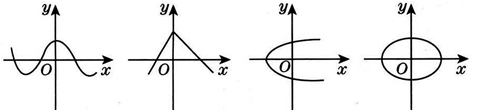 A、1个 B、2个 C、3个 D、4个4. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 = B、 =1 C、(2﹣ )(2+ )=1 D、6. 下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )A、 B、 C、 D、7. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、8. 如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( )
A、1个 B、2个 C、3个 D、4个4. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、5. 下列计算正确的是( )A、 = B、 =1 C、(2﹣ )(2+ )=1 D、6. 下列各组数据分别是三角形的三边长,其中不能构成直角三角形的是( )A、 B、 C、 D、7. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、8. 如图,CB=1,且OA=OB,BC⊥OC,则点A在数轴上表示的实数是( ) A、 B、﹣ C、 D、﹣9. 如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( )
A、 B、﹣ C、 D、﹣9. 如图,某自动感应门的正上方A处装着一个感应器,离地AB=2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开.一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于( ) A、1.2米 B、1.5米 C、2.0米 D、2.5米10. 如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )
A、1.2米 B、1.5米 C、2.0米 D、2.5米10. 如图是放在地面上的一个长方体盒子,其中AB=9cm,BC=6cm,BF=5cm,点M在棱AB上,且AM=3cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为( )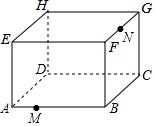 A、10cm B、 C、 D、9cm
A、10cm B、 C、 D、9cm二、填空题
-
11. 若函数 是一次函数,则m的值为 .12. 已知鞋子的“码”数与“厘米”数的对应关系如下:
码
35
36
37
38
39
40
…
厘米
22.5
23
23.5
24
24.5
25
…
设鞋子的“码”数为x,长度为y(厘米),那么y与x之间的关系式是 .
13. 如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”P到y轴的距离为3,则P点的坐标为 .14. 如图,在平面直角坐标系中有一个长方形ABCO,C点在x轴上,A点在y轴上,B点坐标(8,4),将长方形沿EF折叠,使点B落到原点O处,点C落到点D处,则OF的长度是.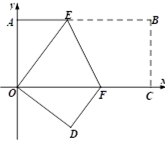 15. 观察下列一组数:
15. 观察下列一组数:列举:3,4,5, 猜想:32=4+5;
列举:5,12,13,猜想:52=12+13;
列举:7,24,25,猜想:72=24+25;
… …
列举:13,b , c , 猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= , c= .
三、解答题
-
16. 计算:(1)、(2)、(3)、(4)、17. 已知x=2﹣ ,y=2+ ,求:x2+xy+y2的值.18. 如图所示,△ABC在正方形网格中,若点A的坐标为(0,3),按要求回答下列问题:
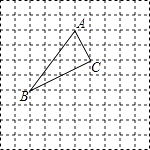 (1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出点B和点C的坐标;(3)、作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)19. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)、在图中建立正确的平面直角坐标系;(2)、根据所建立的坐标系,写出点B和点C的坐标;(3)、作出△ABC关于x轴的对称图形△A′B′C′.(不用写作法)19. 如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形. (1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个三角形,使它的三边长分别为 ;(3)、在图3中,画一个三角形,使它的面积为5.20. 求代数式 的值,其中 .如图是小亮和小芳的解答过程.
(1)、在图1中,画一个三角形,使它的三边长都是有理数;(2)、在图2中,画一个三角形,使它的三边长分别为 ;(3)、在图3中,画一个三角形,使它的面积为5.20. 求代数式 的值,其中 .如图是小亮和小芳的解答过程.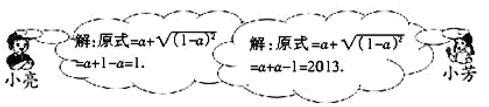 (1)、的解法是错误的;(2)、错误的原因在于未能符合题意地运用二次根式的性质:;(3)、求代数式 的值,其中 .21. 某种子商店销售玉米种子,为惠民促销,推出两种销售方案供采购者选择.
(1)、的解法是错误的;(2)、错误的原因在于未能符合题意地运用二次根式的性质:;(3)、求代数式 的值,其中 .21. 某种子商店销售玉米种子,为惠民促销,推出两种销售方案供采购者选择.方案一:每千克种子价格为4元,无论购买多少均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次性购买超过3千克的,则超过3千克的部分的种子价格打7折.
(1)、请分别求出方案一和方案二中购买的种子数量x(千克)(x>3)和付款金额y(元)之间的函数关系式;(2)、王伯伯要买20千克玉米种子,选哪种方案合适?说明理由.(3)、李叔叔买花了36元,最多可买多少千克玉米种子?22. 如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度.于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如右图为示意图).请你帮小旭求出风筝距离地面的高度AB. 23. 如图
23. 如图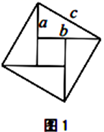
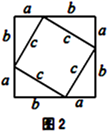

(背景阅读)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了验证勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.
(实践操作)
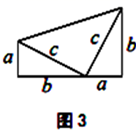
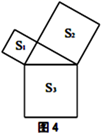
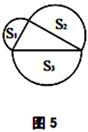
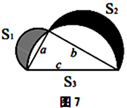
(1)、请叙述勾股定理;(2)、验证勾股定理,人们已经找到了400多种方法,请从下列几种常见的验证方法中任选一种来验证该定理:(以下图形均满足验证勾股定理所需的条件)(3)、(探索发现)如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足 的有个;(4)、如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为 、 ,直角三角形面积为 ,请判断 、 、 的关系并说明理由.