四川省绵阳市三台县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-30 类型:期末考试
一、单选题
-
1. 如图所示的标志中,是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm3. 如图, ,则图中全等三角形共有( )
A、1个 B、2个 C、3个 D、4个2. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm3. 如图, ,则图中全等三角形共有( )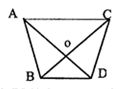 A、1对 B、2对 C、3对 D、4对4. 如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成30°角,这棵树在折断前的高度是( )
A、1对 B、2对 C、3对 D、4对4. 如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成30°角,这棵树在折断前的高度是( )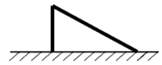 A、5m B、10m C、15m D、20m5. 如图,AD是△ABC的边BC上的中线,BE是△ABD的边AD上的中线,若△ABC的面积是16,则△ABE的面积是( )
A、5m B、10m C、15m D、20m5. 如图,AD是△ABC的边BC上的中线,BE是△ABD的边AD上的中线,若△ABC的面积是16,则△ABE的面积是( )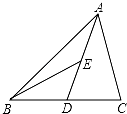 A、16 B、8 C、4 D、26. 下列运算正确的是( )A、 B、 C、 D、7. 分式 中的x、y同时扩大2倍,则分式值( )A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的8. 如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于点F,若BF=AC,则∠ABC等于( )
A、16 B、8 C、4 D、26. 下列运算正确的是( )A、 B、 C、 D、7. 分式 中的x、y同时扩大2倍,则分式值( )A、不变 B、是原来的2倍 C、是原来的4倍 D、是原来的8. 如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于点F,若BF=AC,则∠ABC等于( )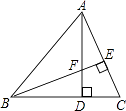 A、45° B、48° C、50° D、60°9. 如图①,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图②),利用这两个图形的面积,可以验证的等式是( )
A、45° B、48° C、50° D、60°9. 如图①,在边长为a的正方形中剪去一个边长为b(b<a)的小正方形,把剩下部分拼成一个梯形(如图②),利用这两个图形的面积,可以验证的等式是( ) A、a2+b2=(a+b)(a-b) B、(a-b)2=a2-2ab+b2 C、(a+b)2=a2+2ab+b2 D、a2-b2=(a+b)(a-b)10. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、 D、11. 若 ,则 的值是 ( )A、 B、 C、3 D、612. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数( )
A、a2+b2=(a+b)(a-b) B、(a-b)2=a2-2ab+b2 C、(a+b)2=a2+2ab+b2 D、a2-b2=(a+b)(a-b)10. 对于实数 、 ,定义一种新运算“ ”为: ,这里等式右边是实数运算.例如: .则方程 的解是( )A、 B、 C、 D、11. 若 ,则 的值是 ( )A、 B、 C、3 D、612. 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,下列结论:①CD=ED;②AC+BE=AB;③∠BDE=∠BAC;④BE=DE;⑤SBDE:S△ACD=BD:AC,其中正确的个数( )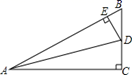 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
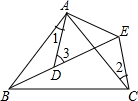
13. 点(2+a,3)关于y轴对称的点的坐标是(﹣4,2﹣b),则ab= .14. 分解因式:ab2﹣4ab+4a= .15. 如图所示,AB=AC , AD=AE , ∠BAC=∠DAE , ∠1=25°,∠2=30°,则∠3= .
 16. 如图, 中, , ,DE是BC边上的垂直平分线, 的周长为14cm,则 的面积是 .
16. 如图, 中, , ,DE是BC边上的垂直平分线, 的周长为14cm,则 的面积是 .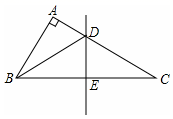 17. 某特快列车在最近一次的铁路大提速后,时速提高了30千米/小时,则该列车行驶350千米所用的时间比原来少用1小时,若该列车提速前的速度是 千米/小时,根据题意可列方程为 .18. 观察下列各式: , , ,请利用上述规律计算: ( 为正整数).
17. 某特快列车在最近一次的铁路大提速后,时速提高了30千米/小时,则该列车行驶350千米所用的时间比原来少用1小时,若该列车提速前的速度是 千米/小时,根据题意可列方程为 .18. 观察下列各式: , , ,请利用上述规律计算: ( 为正整数).三、解答题
-
19. 计算题(1)、计算:(2)、先化简,再求值: ,其中 .20. 如图,在平面直角坐标系中,
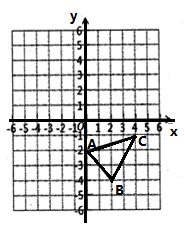 (1)、作出 关于 轴对称的 ,并写出 三个顶点的坐标;(2)、请计算 的面积;21. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ),点 在 上,点 和 分别与木墙的顶端重合.
(1)、作出 关于 轴对称的 ,并写出 三个顶点的坐标;(2)、请计算 的面积;21. 王强同学用10块高度都是 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板( ),点 在 上,点 和 分别与木墙的顶端重合.
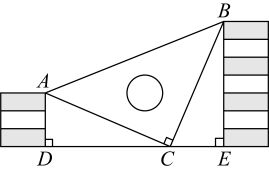 (1)、求证: ;(2)、求两堵木墙之间的距离.22. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2015年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2018年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?23. 如图,在 中, , 为 上一点, , 于点 , 于点 , 相交于点 .
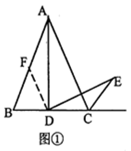
(1)、求证: ;(2)、求两堵木墙之间的距离.22. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2015年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2018年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?23. 如图,在 中, , 为 上一点, , 于点 , 于点 , 相交于点 . (1)、求证: ;(2)、若 ,求 的长.24. 回答下列问题:(1)、问题情境:小明遇到这样一个问题:如图①,已知 是等边三角形,点 为 边上中点, , 交等边三角形外角平分线 所在的直线于点 ,试探究 与 的数量关系.
(1)、求证: ;(2)、若 ,求 的长.24. 回答下列问题:(1)、问题情境:小明遇到这样一个问题:如图①,已知 是等边三角形,点 为 边上中点, , 交等边三角形外角平分线 所在的直线于点 ,试探究 与 的数量关系.小明发现:过 作 ,交 于 ,构造全等三角形,经推理论证问题得到解决.请直接写出 与 的数量关系,并说明理由.
 (2)、类比探究:如图②,当 是线段 上(除 外)任意一点时(其他条件不变)试猜想 与 的数量关系并证明你的结论.
(2)、类比探究:如图②,当 是线段 上(除 外)任意一点时(其他条件不变)试猜想 与 的数量关系并证明你的结论.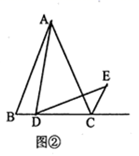 (3)、拓展应用:当 是线段 上延长线上,且满足 (其他条件不变)时,请判断 的形状,并说明理由.
(3)、拓展应用:当 是线段 上延长线上,且满足 (其他条件不变)时,请判断 的形状,并说明理由.