四川省达州市开江县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-30 类型:期末考试
一、单选题
-
1. 的算术平方根是( )
A、3 B、 C、±3 D、±2. 下列各数组中,不是勾股数的是( )A、 , , B、 , , C、 , , D、 , , ( 为正整数)3. 下列运算正确的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人参加射击训练,经过三组练习,他们的平均成绩都是 环,方差分别是 , , , ,你认为谁的成绩更稳定( )A、甲 B、乙 C、丙 D、丁5. 已知直线 ,将一块含 角的直角三角板( )按如图所示的位置摆放,若 , 则 的度数为( ) A、 B、 C、 D、6. 下列命题中是真命题的是( )A、平面内,过一点有且只有一条直线与已知直线平行 B、 , , , , …等五个数都是无理数 C、若 ,则点 在第二象限 D、若三角形的边 、 、 满足: ,则该三角形是直角三角形7. 直线 的图象如图所示,则函数 的图象大致是( )
A、 B、 C、 D、6. 下列命题中是真命题的是( )A、平面内,过一点有且只有一条直线与已知直线平行 B、 , , , , …等五个数都是无理数 C、若 ,则点 在第二象限 D、若三角形的边 、 、 满足: ,则该三角形是直角三角形7. 直线 的图象如图所示,则函数 的图象大致是( ) A、
A、 B、
B、 C、
C、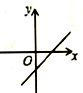 D、
D、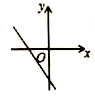 8. 某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练少 个,一个学徒工与两个熟练工每天共可制造 个零件,求一个学徒工与 一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造 个零件,一个熟练工每天能制造 个零件,根据题意可列方程组为( )A、 B、 C、 D、9. 一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为 (小时),两车之间的距离为 (千米),如图中的折线表示 与 之间的函数关系,下列说法:①动车的速度是 千米/小时;②点B的实际意义是两车出发后 小时相遇;③甲、乙两地相距 千米;④普通列车从乙地到达甲地时间是 小时,其中错误的有( )
8. 某公司有学徒工和熟练工两个工种的工人,已知一个学徒工每天制造的零件比一个熟练少 个,一个学徒工与两个熟练工每天共可制造 个零件,求一个学徒工与 一个熟练工每天各能制造多少个零件?设一个学徒工每天能制造 个零件,一个熟练工每天能制造 个零件,根据题意可列方程组为( )A、 B、 C、 D、9. 一列动车从甲地开往乙地, 一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为 (小时),两车之间的距离为 (千米),如图中的折线表示 与 之间的函数关系,下列说法:①动车的速度是 千米/小时;②点B的实际意义是两车出发后 小时相遇;③甲、乙两地相距 千米;④普通列车从乙地到达甲地时间是 小时,其中错误的有( ) A、 个 B、 个 C、 个 D、 个10. 若将一副三角板按如图所示的方式放置,则下列结论:① ;②如果 ,则有 ;③如果 ,则有 ;④如果 ,必有 ;其中正确的有( )
A、 个 B、 个 C、 个 D、 个10. 若将一副三角板按如图所示的方式放置,则下列结论:① ;②如果 ,则有 ;③如果 ,则有 ;④如果 ,必有 ;其中正确的有( ) A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
11. 已知 ,则 的值是 .12. 如图所示,一次函数y=ax+b的图象与x轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
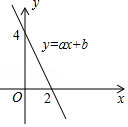 13. 若点 关于 轴的对称点 的坐标是 ,则 的值是 .14. 如图,在 中, , , ,分别以点 , 为圆心,大于 的长为半径画弧,两弧交点分别为点 , ,过 , 两点作直线交 于点 ,则 的长是 .
13. 若点 关于 轴的对称点 的坐标是 ,则 的值是 .14. 如图,在 中, , , ,分别以点 , 为圆心,大于 的长为半径画弧,两弧交点分别为点 , ,过 , 两点作直线交 于点 ,则 的长是 . 15. 对于实数a,b,定义运算“※”:a※b= ,例如3※4,因为3<4.所以3※4=3×4=12.若x,y满足方程组 ,则x※y= .16. 如图,直线 : ,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ;…,按此作法进行下去.点 的坐标为 .
15. 对于实数a,b,定义运算“※”:a※b= ,例如3※4,因为3<4.所以3※4=3×4=12.若x,y满足方程组 ,则x※y= .16. 如图,直线 : ,点 的坐标为 ,过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ;再过点 作 轴的垂线交直线 于点 ,以原点 为圆心, 长为半径画弧交 轴负半轴于点 ;…,按此作法进行下去.点 的坐标为 .
三、解答题
-
17.(1)、计算题:(2)、解方程组:18. 某县教育行政部门为了了解八年级学生每学期参加综合实践活动的情况,随机抽样调查了该县八年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).

请你根据图中提供的信息,回答下列问题:
(1)、求出参加抽样调查的八年级学生人数,并将频数直方图补充完整.(2)、在这次抽样调查中,众数和中位数分别是多少?(3)、如果该县共有八年级学生 人,请你估计“活动时间不少于 天”的大约有多少人?19. 在平面直角坐标系中,有点 , .(1)、若线段 轴,求点 、 的坐标;(2)、当点 到 轴的距离与点 到 轴的距离相等时,求点 所在的象限.20. 如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2. (1)、求证:AB∥CD;(2)、若FG⊥BC于点H,BC平分∠ABD,∠D=112°,求∠1的度数.21. 某超市第一次用 元购进甲、乙两种商品,其中甲商品件数的 倍比乙商品件数的 倍多 件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)
(1)、求证:AB∥CD;(2)、若FG⊥BC于点H,BC平分∠ABD,∠D=112°,求∠1的度数.21. 某超市第一次用 元购进甲、乙两种商品,其中甲商品件数的 倍比乙商品件数的 倍多 件,甲、乙两种商品的进价和售价如下表(利润=售价-进价)甲
乙
进价(元/件)
20
28
售价(元/件)
26
40
(1)、该超市第一次购进甲、乙两种商品的件数分别是多少?(2)、该超市将第一次购进的甲、 乙两种商品全部卖出后一共可获得多少利润?(3)、该超市第二次以同样的进价又购进甲、乙两种商品.其中甲商品件数是第一次的2倍,乙商品的件数不变.甲商品按原价销售,乙商品打折销售.第二次甲、乙两种商品销售完以后获得的利润比第一次获得的利润多 元,则第二次乙商品是按原价打几折销售的?22. 在甲村至乙村的公路旁有一块山地正在开发,现有一 处需要爆破.已知点 与公路上的停靠站 的距离为 米,与公路上另一停靠站 的距离为 米,且 ,如图,为了安全起见,爆破点 周围半径 米范围内不得进入,问在进行爆破时,公路 段是否有危险,是否需要暂时封锁?请通过计算进行说明. 23. 先观察下列等式,再回答问题:
23. 先观察下列等式,再回答问题:① ;
② ;
③ ;
(1)、根据上面三个等式,请猜想 的结果(2)、根据上述规律,解答问题:设 ,求不超过 的最大整数是多少?
24. 问题发现:如图 ,在 中, , 为 边所在直线上的动点(不与点 、 重合),连结 ,以 为边作 ,且 ,根据 ,得到 ,结合 , 得出 ,发现线段 与 的数量关系为 ,位置关系为 ; (1)、探究证明:如图 ,在 和 中, , ,且点 在 边上滑动(点 不与点 、 重合),连接 .
(1)、探究证明:如图 ,在 和 中, , ,且点 在 边上滑动(点 不与点 、 重合),连接 .①求线段 , , 之间满足的等量关系式;
②求证: ;
(2)、拓展延伸:如图 ,在四边形 中, .若 , ,求 的长.25. 如图 ,已知直线 与 轴, 轴分别交于 , 两点,以 为直角顶点在第二象限作等腰 . (1)、求点 的坐标,并求出直线 的关系式;(2)、如图 ,直线 交 轴于 ,在直线 上取一点 ,连接 ,若 ,求证: .(3)、如图 ,在(1)的条件下,直线 交 轴于点 , 是线段 上一点,在 轴上是否存在一点 ,使 面积等于 面积的一半?若存在,请求出点 的坐标;若不存在,请说明理由.
(1)、求点 的坐标,并求出直线 的关系式;(2)、如图 ,直线 交 轴于 ,在直线 上取一点 ,连接 ,若 ,求证: .(3)、如图 ,在(1)的条件下,直线 交 轴于点 , 是线段 上一点,在 轴上是否存在一点 ,使 面积等于 面积的一半?若存在,请求出点 的坐标;若不存在,请说明理由.