四川省成都市新都区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{25}$ 的算术平方根是（　　）

A、5 B、﹣5 C、 $\sqrt{5}$ D、 $\pm \sqrt{5}$

查看试题解析
2. 下列实数中的无理数是（）

A、﹣ $\frac{1}{3}$ B、π C、0.57 D、 $\frac{22}{7}$

查看试题解析
3. 在平面直角坐标系中，点P（4，3）关于原点对称的点的坐标为（）

A、（﹣4，﹣3） B、（﹣4，3） C、（3，﹣4） D、（﹣3，4）

查看试题解析
4. 对于函数y＝2x+1下列结论错误的是（）

A、它的图象必过点（1，3） B、它的图象经过一、二、三象限 C、当x＞ $\frac{1}{2}$ 时，y＞0 D、y值随x值的增大而增大

查看试题解析
5. 如图，已知一次函数 $y = k x + b$ 的图象经过A（0，1）和B（2，0），当x＞0时， y的取值范围是（）

A、 $y < 1$ ； B、 $y < 0$ ； C、 $y > 1$ ； D、 $y < 2$

查看试题解析
6. 以下列三个数据为三角形的三边，其中能构成直角三角形的是（）

A、2，3，4 B、4，5，6 C、5，12，13 D、5，6，7

查看试题解析
7. 要使二次根式 $\sqrt{2 - x}$ 有意义，字母x必须满足的条件是（）

A、x≤2 B、x＜2 C、x≤－2 D、x＜－2

查看试题解析
8. 下列命题是真命题的是（）

A、中位数就是一组数据中最中间的一个数 B、一组数据的众数可以不唯一 C、一组数据的标准差就是这组数据的方差的平方根 D、已知a、b、c是Rt△ABC的三条边，则a²+b²＝c²

查看试题解析
9. 若函数y=（m-1）x^∣^m^∣-5是一次函数，则m的值为（）

A、±1 B、-1 C、1 D、2

查看试题解析
10.
如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（　　）

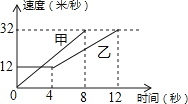A、乙前4秒行驶的路程为48米 B、在0到8秒内甲的速度每秒增加4米/秒 C、两车到第3秒时行驶的路程相等 D、在4至8秒内甲的速度都大于乙的速度

查看试题解析

二、填空题

11. 若|3x+2y+1|+ $\sqrt{x + y - 5}$ ＝0，则x﹣y＝

查看试题解析
12. 点M（3，﹣1）到x轴距离是．

查看试题解析
13. 如图，将一张长方形纸片分别沿着EP、FP对折，使点A落在点A′，点B落在点B′，若点P，A′，B′在同一直线上，则两条折痕的夹角∠EPF的度数为．

查看试题解析
14.
如图，A、B的坐标分别为（2，0）、（0，1），若将线段AB平移至A₁B₁ ， A₁、B₁的坐标分别为（3，1）、（a，b），则a+b的值为

查看试题解析
15.
如图，正方形ODBC中，OB= $\sqrt{2}$ ， OA=OB，则数轴上点A表示的数是

查看试题解析
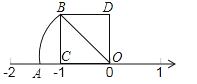16. 已知：如图，在平面直角坐标系xOy中，一次函数y＝ $\frac{3}{4}$ x+3的图象与x轴和y轴交于A、B两点将△AOB绕点O顺时针旋转90°后得到△A′OB′则直线A′B′的解析式是．

查看试题解析
17. 对于实数x，我们规定[X）表示大于x的最小整数，如[4）═5，[ $\sqrt{3}$ ）=2，[﹣2.5）=﹣2，现对64进行如下操作：
64 $\underset{\to}{第 1 次}$ [ $\sqrt{64}$ ）=9 $\underset{\to}{第 2 次}$ [ $\sqrt{9}$ ）="4" $\underset{\to}{第 3 次}$ [ $\sqrt{4}$ ）=3 $\underset{\to}{第 4 次}$ [[ $\sqrt{3}$ ）=2，

这样对64只需进行4次操作后变为2，类似地，只需进行4次操作后变为2的所有正整数中，最大的是．

查看试题解析
18. 如图，长方形ABCD中AB＝2，BC＝4，正方形AEFG的边长为1．正方形AEFG绕点A旋转的过程中，线段CF的长的最小值为．

查看试题解析
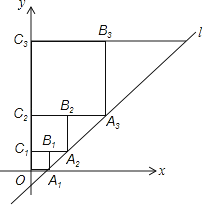
19.
在平面直角坐标系中，直线l：y=x﹣1与x轴交于点A₁ ，如图所示依次作正方形A₁B₁C₁O、正方形A₂B₂C₂C₁、…、正方形A_nB_nC_nC_n_﹣₁ ，使得点A₁、A₂、A₃、…在直线l上，点C₁、C₂、C₃、…在y轴正半轴上，则点B_n的坐标是．

查看试题解析

三、解答题

20. 计算：

(1)、（ $\sqrt{12} + \sqrt{20}$ ）+（ $\sqrt{3} - \sqrt{5}$ ）

(2)、 $\sqrt{4} - (\frac{1}{\sqrt{5} - 2}) + {(- 2)}^{3} \div \frac{1}{3}$

查看试题解析
21. 解方程组：

(1)、 ${\begin{array}{l} 3 x - y = 2 \\ 9 x + 8 y = 17 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{2} + 2 y = 7 \\ 2 x + \frac{y}{3} = 5 \end{array}$

查看试题解析

22. 小冬与小夏是某中学篮球队的队员，在最近五场球赛中的得分如下表所示：

	第一场	第二场	第三场	第四场	第五场
小冬	10	13	9	8	10
小夏	12	2	13	21	2

(1)、根据上表所给的数据，填写下表：

	平均数	中位数	众数	方差
小冬	10		10	2.8
小夏	10	12		32.4

(2)、根据以上信息，若教练选择小冬参加下一场比赛，教练的理由是什么？

(3)、若小冬的下一场球赛得分是11分，则在小冬得分的四个统计量中（平均数、中位数、众数与方差）哪些发生了改变，改变后是变大还是变小？（只要回答是“变大”或“变小”）

（ $S^{2} = \frac{1}{n} [{(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}]$ ）

查看试题解析

23. 已知a，b，c满足 $\sqrt{8 - a} + \sqrt{a - 8}$ ＝|c﹣17|+b²﹣30b+225，

(1)、求a，b，c的值；

(2)、试问以a，b，c为边能否构成三角形？若能构成三角形，求出三角形的周长和面积；若不能构成三角形，请说明理由．

查看试题解析
24. 如图，已知直线y=kx+b交x轴于点A，交y轴于点B，直线y=2x﹣4交x轴于点D，与直线AB相交于点C（3，2）．

(1)、根据图象，写出关于x的不等式2x﹣4＞kx+b的解集；

(2)、若点A的坐标为（5，0），求直线AB的解析式；

(3)、在（2）的条件下，求四边形BODC的面积．

查看试题解析
25. 如图1，在正方形ABCD（正方形四边相等，四个角均为直角）中，AB＝8，P为线段BC上一点，连接AP，过点B作BQ⊥AP，交CD于点Q，将△BQC沿BQ所在的直线对折得到△BQC′，延长QC′交AD于点N．

(1)、求证：BP＝CQ；

(2)、若BP＝ $\frac{1}{3}$ PC，求AN的长；

(3)、如图2，延长QN交BA的延长线于点M，若BP＝x（0＜x＜8），△BMC'的面积为S，求S与x之间的函数关系式．

查看试题解析
26. 某服务厂生产一种西装和领带，西装每套定价200元，领带每条定价40元．厂方在开展促销活动期间，向客户提供两种优惠方案：（I）买一套西装送一条领带；（II）西装和领带均按定价的90%付款．某超市经理现要到该服务厂购买西装20套，领带若干条（不少于20条）．

(1)、设购买领带为x（条），采用方案I购买时付款数为y₁（元），采用方案II购买时付款数为 $y_{I I}$ （元）．分别写出采用两种方案购买时付款数与领带条数x之间的函数关系式；

(2)、就领带条数x讨论在上述方案中采用哪种方案购买合算．

查看试题解析
27. 如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，点D在边AB上，点E在边AC的左侧，连接AE．

(1)、求证：AE＝BD；

(2)、试探究线段AD、BD与CD之间的数量关系；

(3)、过点C作CF⊥DE交AB于点F，若BD：AF＝1：2 $\sqrt{2}$ ，CD＝ $\sqrt{3} + \sqrt{6}$ ，求线段AB的长．

查看试题解析
28. 如图 1，在平面直角坐标系中，直线l₁：y=-x+5与x轴，y轴分别交于A．B两点.直线l₂：y=-4x+b与l₁交于点 D(－3，8)且与x轴，y轴分别交于C、E.

(1)、求出点A坐标，直线l₂的解析式；

(2)、如图2，点P为线段AD上一点(不含端点)，连接CP，一动点Q从C出发，沿线段CP 以每秒1个单位的速度运动到点P，再沿着线段PD以每秒 $\sqrt{2}$ 个单位的速度运动到点D停止，求点Q在整个运动过程中所用最少时间与点P的坐标；

(3)、如图3，平面直角坐标系中有一点G(m，2)，使得S_D_CEG=S_D_CEB ，求点G的坐标.

查看试题解析