四川省成都市武侯区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $\sqrt[3]{8}$ ，0， $\frac{π}{2}$ ，﹣ $\frac{22}{7}$ ，0.1010010001…（相邻两个1之间的0的个数逐渐增加1）这六个数中，无理数的个数共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 在平面直角坐标系中，点P（﹣ $\sqrt{5}$ ，﹣2）关于原点对称的点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ = $\sqrt{5}$ B、 $\sqrt{8}$ =4 $\sqrt{2}$ C、3 $\sqrt{2}$ ﹣ $\sqrt{2}$ =3 D、 $\sqrt{2}$ $\cdot \sqrt{3}$ = $\sqrt{6}$

查看试题解析
4. 在平面直角坐标系中，直线y＝2x﹣3与y轴的交点坐标是（）

A、（0，﹣3） B、（﹣3，0） C、（2，﹣3） D、（ $\frac{3}{2}$ ，0）

查看试题解析
5. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是一次函数y＝﹣ $\frac{2}{3}$ x+5图象上的两个点，且x₁＜x₂ ，则y₁与y₂的大小关系是（）

A、y₁＝y₂ B、y₁＜y₂ C、y₁＞y₂ D、无法确定

查看试题解析
6. 下列说法正确的是（）

A、 $\sqrt{9}$ 的算术平方根是3 B、平行于同一条直线的两条直线互相平行 C、带根号的数都是无理数 D、三角形的一个外角大于任意一个内角

查看试题解析
7. 如图，在平面直角坐标系中，已知点A（﹣2，0），B（0，3），以点A为圆心，AB长为半径画弧，交x轴的正半轴于点C，则点C的横坐标介于（）

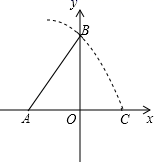A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间

查看试题解析
8. 武侯区初中数学分享学习课堂改革正在积极推进，在一次数学测试中，某班的一个共学小组每位同学的成绩（单位：分；满分100分）分别是：92，90，94，88，记这组数据的方差为 $S_{1}^{2}$ ．将上面这组数据中的每一个数都减去90，得到一组新数据2，0，4，﹣2，记这组新数据的方差为 $S_{2}^{2}$ ，此时有 $S_{1}^{2}$ ＝ $S_{2}^{2}$ ，则 $S_{1}^{2}$ 的值为（）

A、1 B、2 C、4 D、5

查看试题解析
9. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题：“一条竿子一条索，索比竿子长一托．折回索子却量竿，却比竿子短一托“其大意为：现有一根竿和一条绳索，用绳索去量竿，绳索比竿长5尺；如果将绳索对半折后再去量竿，就比竿短5尺．设绳索长x尺，竿长y尺，则正确的方程组是（）

A、 ${\begin{cases} x = y + 5 \\ \frac{1}{2} x = y - 5 \end{cases}$ B、 ${\begin{cases} x = y + 5 \\ \frac{1}{2} x = y + 5 \end{cases}$ C、 ${\begin{cases} x = y + 5 \\ 2 x = y - 5 \end{cases}$ D、 ${\begin{cases} x = y - 5 \\ 2 x = y + 5 \end{cases}$

查看试题解析
10. 如图，在长方形ABCD中，AB＝6，BC＝8，∠ABC的平分线交AD于点E，连接CE，过B点作BF⊥CE于点F，则BF的长为（）

A、 $\frac{5 \sqrt{10}}{12}$ B、 $\frac{5 \sqrt{10}}{6}$ C、 $\frac{12 \sqrt{10}}{5}$ D、 $\frac{6 \sqrt{10}}{5}$

查看试题解析

二、填空题

11. 已知x，y满足方程组 ${\begin{array}{l} 3 x - y = 10 \\ 3 x + y = 8 \end{array}$ ，则9x²﹣y²的值为．

查看试题解析
12. 如图，将直线OA向上平移3个单位长度，则平移后的直线的表达式为．

查看试题解析
13. 如图，∠BCD是△ABC的外角，CE平分∠BCD，若AB＝AC，∠ECD＝52.5°，则∠A的度数为．

查看试题解析
14. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AB＝4 $\sqrt{3}$ cm，动点P从点B出发沿射线BC方向以2cm/s的速度运动．设运动的时间为t秒，则当t＝秒时，△ABP为直角三角形．

查看试题解析
15. 已知x是 $\sqrt{7}$ 的整数部分，y是 $\sqrt{7}$ 的小数部分，则xy的值．

查看试题解析
16. 若实数a，b满足 $\sqrt{a - 5} + 2 \sqrt{5 - a} = b + 4$ ，则a﹣b的平方根是．

查看试题解析
17. 如图，把平面内一条数轴x绕点O逆时针旋转角θ（0°＜θ＜90°）得到另一条数轴y，x轴和y轴构成一个平面斜坐标系.规定：已知点P是平面斜坐标系中任意一点，过点P作y轴的平行线交x轴于点A，过点P作x轴的平行线交y轴于点B，若点A在x轴上对应的实数为a，点B在y轴上对应的实数为b，则称有序实数对（a，b）为点P的斜坐标.在平面斜坐标系中，若θ＝45°，点P的斜坐标为（1，2 $\sqrt{2}$ ），点G的斜坐标为（7，﹣2 $\sqrt{2}$ ），连接PG，则线段PG的长度是.

查看试题解析
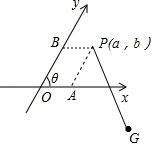18. 如图，在△ABC中，∠A＝90°，AB＝2 $\sqrt{5}$ ，AC＝ $\sqrt{5}$ ，以BC为斜边作等腰Rt△BCD，连接AD，则线段AD的长为．

查看试题解析
19. 如图，在正方形网格中，△ABC的每一个顶点都在格点上，AB＝5，点D是AB边上的动点（点D不与点A，B重合），将线段AD沿直线AC翻折后得到对应线段AD₁ ，将线段BD沿直线BC翻折后得到对应线段BD₂ ，连接D₁D₂ ，则四边形D₁ABD₂的面积的最小值是．

查看试题解析

三、解答题

20. 计算

(1)、 $\sqrt{20}$ +|2﹣ $\sqrt{5}$ |﹣ $\sqrt[3]{- 27}$ ﹣（π﹣ $\sqrt{7}$ ）⁰

(2)、（ $\sqrt{12}$ ﹣2 $\sqrt{7}$ ）× $\sqrt{3}$ +3 $\sqrt{\frac{7}{3}}$

查看试题解析
21.

(1)、解方程 ${\begin{array}{l} 2 x + 4 y = 16 \\ 5 x - 2 y = 4 \end{array}$

(2)、在（1）的基础上，求方程组 ${\begin{array}{l} 2 (m + n) + 4 (m - n) = 16 \\ 5 (m + n) - 2 (m - n) = 4 \end{array}$ 的解．

查看试题解析
22. 某公司销售部有营销员15人，销售部为了制定关于某种商品的每位营销员的个人月销售定额，统计了这15人某月关于此商品的个人月销售量（单位：件）如下：

个人月销售量

1800

510

250

210

150

120

营销员人数

1

1

3

5

3

2

(1)、求这15位营销员该月关于此商品的个人月销售量的平均数，并直接写出这组数据的中位数和众数；

(2)、假设该销售部负责人把每位营销员关于此商品的个人月销售定额确定为320件，你认为对多数营销员是否合理？并在（1）的基础上说明理由．

查看试题解析
23. 如图，在平面直角坐标系xOy中，已知△OAB的两个顶点的坐标分别是A（3，0），B（2，3）．

(1)、画出△OAB关于y轴对称的△OA₁B₁ ，其中点A，B的对应点分别为A₁ ， B₁ ，并直接写出点A₁ ， B₁的坐标；

(2)、点C为y轴上一动点，连接A₁C，B₁C，求A₁C+B₁C的最小值并求出此时点C的坐标．

查看试题解析
24. 如图，△ABC是等腰直角三角形，且∠ACB＝90°，点D是AB边上的一点（点D不与A，B重合），连接CD，过点C作CE⊥CD，且CE＝CD，连接DE，AE．

(1)、求证：△CBD≌△CAE；

(2)、若AD＝4，BD＝8，求DE的长．

查看试题解析
25. 如图，过点A（1，3）的一次函数y＝kx+6（k≠0）的图象分别与x轴，y轴相交于B，C两点．

(1)、求k的值；

(2)、直线l与y轴相交于点D（0，2），与线段BC相交于点E．
（i）若直线l把△BOC分成面积比为1：2的两部分，求直线l的函数表达式；

（ⅱ）连接AD，若△ADE是以AE为腰的等腰三角形，求满足条件的点E的坐标．

查看试题解析
26. 某市为了鼓励居民在枯水期（当年11月至第二年5月）节约用电，规定7：00至23：00为用电高峰期，此期间用电电费y₁（单位：元）与用电量x（单位：度）之间满足的关系如图所示；规定23：00至第二天早上7：00为用电低谷期，此期间用电电费y₂（单位：元）与用电量x（单位：元）之间满足如表所示的一次函数关系．

(1)、求y₂与x的函数关系式；并直接写出当0≤x≤180和x＞180时，y₁与x的函数关系式；

(2)、若市民王先生一家在12月份共用电350度，支付电费150元，求王先生一家在高峰期和低谷期各用电多少度．

低谷期用电量x度

…

80

100

140

…

低谷期用电电费y₂元

…

20

25

35

…

查看试题解析
27. 如图，AC平分钝角∠BAE交过B点的直线于点C，BD平分∠ABC交AC于点D，且∠BAD+∠ABD＝90°．

(1)、求证：AE∥BC；

(2)、点F是射线BC上一动点（点F不与点B，C重合），连接AF，与射线BD相交于点P．
（ⅰ）如图1，若∠ABC＝45°，AF⊥AB，试探究线段BF与CF之间满足的数量关系；

（ⅱ）如图2，若AB＝10，S△ABC＝30，∠CAF＝∠ABD，求线段BP的长．

查看试题解析
28. 如图，在平面直角坐标系中，直线y＝﹣ $\frac{\sqrt{3}}{3}$ x+3分别交y轴，x轴于A、B两点，点C在线段AB上，连接OC，且OC＝BC．

(1)、求线段AC的长度；

(2)、如图2，点D的坐标为（﹣ $\sqrt{3}$ ，0），过D作DE⊥BO交直线y＝﹣ $\frac{\sqrt{3}}{3}$ x+3于点E．动点N在x轴上从点D向终点O匀速运动，同时动点M在直线＝﹣ $\frac{\sqrt{3}}{3}$ x+3上从某一点向终点G（2 $\sqrt{3}$ ，1）匀速运动，当点N运动到线段DO中点时，点M恰好与点A重合，且它们同时到达终点．
i）当点M在线段EG上时，设EM＝s、DN＝t，求s与t之间满足的一次函数关系式；

ii）在i）的基础上，连接MN，过点O作OF⊥AB于点F，当MN与△OFC的一边平行时，求所有满足条件的s的值．

查看试题解析

低谷期用电量x度	…	80	100	140	…
低谷期用电电费y₂元	…	20	25	35	…

个人月销售量	1800	510	250	210	150	120
营销员人数	1	1	3	5	3	2