四川省成都市温江区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点P（﹣3，7）所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 在Rt△ABC中，以两直角边为边长的正方形面积如图所示，则AB的长为（）

A、49 B、 $\sqrt{31}$ C、3 $\sqrt{2}$ D、7

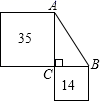查看试题解析
3. 如果m是 $\sqrt{15}$ 的整数部分，则m的值为（）

A、1 B、2 C、3 D、4

查看试题解析
4. 已知点M（a，﹣2）在一次函数y＝3x﹣1的图象上，则a的值为（）

A、﹣1 B、1 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
5. 下列说法正确的是（）

A、16的平方根是4 B、﹣1的立方根是﹣1 C、 $\sqrt{25}$ 是无理数 D、 $\sqrt{9}$ 的算术平方根是3

查看试题解析
6. 如果 ${\begin{array}{l} x = 6 \\ y = - 2 \end{array}$ 是关于xy的二元一次方程mx﹣10＝3y的一个解，则m的值为（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、﹣3 D、﹣2

查看试题解析
7. 某鞋厂为了了解初中生穿鞋的尺码情况，对某中学八年级（2）班的20名男生进行了调查，统计结果如下表：则这20个数据的中位数和众数分别为（）

尺码

37

38

39

40

41

42

人数

3

4

4

7

1

1

A、4和7 B、40和7 C、39和40 D、39.1和39

查看试题解析
8. 下列说法正确的是（）

A、所有命题都是定理 B、三角形的一个外角大于它的任一内角 C、三角形的外角和等于180° D、公理和定理都是真命题

查看试题解析
9. 《孙子算经》中有一道题，原文是：“今有木，不知长短．引绳度之，余绳四足五寸；屈绳量之，不足一尺．木长几何？”意思是：用一根绳子去量一根长木，绳子还剩余 $4.5$ 尺．将绳子对折再量长木，长木还剩余 $1$ 尺，问木长多少尺，现设绳长 $x$ 尺，木长 $y$ 尺，则可列二元一次方程组为（）

A、 ${\begin{array}{l} y - x = 4.5 \\ y - \frac{1}{2} x = 1 \end{array}$ B、 ${\begin{array}{l} x - y = 4.5 \\ y - \frac{1}{2} x = 1 \end{array}$ C、 ${\begin{array}{l} x - y = 4.5 \\ \frac{1}{2} x - y = 1 \end{array}$ D、 ${\begin{array}{l} y - x = 4.5 \\ \frac{1}{2} x - y = 1 \end{array}$

查看试题解析
10. 直线y＝k₁x+b₁（k₁＞0）与y＝k₂x+b₂（k₂＜0）相交于点（﹣3，0），且两直线与y轴围成的三角形面积为12那么b₂﹣b₁的值为（）

A、3 B、8 C、﹣6 D、﹣8

查看试题解析

二、填空题

11. $- \sqrt{6} ， \sqrt{8} ， \sqrt[3]{2} ， \sqrt{\frac{3}{4}}$ 中是最简二次根式的是．

查看试题解析
12. 已知一次函数y＝kx+b（k≠0）的图象与x轴交于（﹣5，0），则关于x的一元一次方程kx+b＝0的解为．

查看试题解析
13. 为从甲乙两名射击运动员中选出一人参加竞标赛，特统计了他们最近10次射击训练的成绩，其中，他们射击的平均成绩为8.9环，方差分别是 $S_{甲}^{2} = 0.8 ， S_{乙}^{2} = 1.3$ ，从稳定性的角度看，的成绩更稳定．（填“甲”或“乙”）

查看试题解析
14. 如图，直线a∥b，∠BAC的顶点A在直线a上，且∠BAC＝98°，若∠1＝35°，则∠2＝度．

查看试题解析
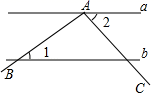15. 如果把人的头顶和脚底分别看作一个点，把地球赤道看作一个圆，那么身高2m的小赵沿着赤道环行一周，他的头顶比脚底多行m．

查看试题解析

三、解答题

16. 解答下列各题

(1)、计算： $\sqrt[3]{- 8} + \sqrt{18} - \sqrt{2} (3 - \sqrt{32})$

(2)、解方程组 ${\begin{array}{l} 2 m - n = - 4 \\ 4 m - 5 n = - 23 \end{array}$

查看试题解析
17. 解答下列各题

(1)、如图1，方格纸中的每个小方格都是边长为1个单位长的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．

①作出△ABC关于x轴对称的△A₁B₁C₁；

②如果P点的纵坐标为3，且P点到直线AA₁的距离为5，请直接写出点P的坐标．

(2)、我国是世界上严重缺水的国家之一为了倡导“节约用水，从我做起”，小丽同学在她家所在小区的200住户中，随机调查了10个家庭在2019年的月均用水量（单位：t），并将调查结果绘成了如下的条形统计图2
①求这10个样本数据的平均数；

②以上面的样本平均数为依据，自来水公司按2019年该小区户月均用水量下达了2020年的用水计划（超计划要执行阶梯式标准收费）请计算该小区2020年的计划用水量．

查看试题解析
18. 解答下列各题

(1)、已知：如图1，直线AB、CD被直线AC所截，点E在AC上，且∠A＝∠D+∠CED，求证：AB∥CD；

(2)、如图2，在正方形ABCD中，AB＝8，BE＝6，DF＝4．
①试判断△AEF的形状，并说明理由；

②求△AEF的面积．

查看试题解析
19. 解答下列各题

(1)、如图1，已知OA＝OB，数轴上的点A所表示的数为m，且|m+n|＝2
①求点A所表示的数m为；

②求代数式n²+m﹣9的值．

(2)、旅客乘车按规定可以随身携带一定质量的行李，如果超过规定，则需购买行李票，设行李票y（元）是行李质量x（千克）的一次函数，其图象如图2所示．
①当旅客需要购买行李票时，求出y与x之间的函数关系式；

②如果张老师携带了42千克行李，她是否要购买行李票？如果购买需买多少行李票？

查看试题解析
20. 某体育文化用品商店购进篮球和排球共200个，进价和售价如下表全部销售完后共获利润2600元．

类别

价格

篮球

排球

进价（元/个）

80

50

售价（元/个）

95

60

(1)、求商店购进篮球和排球各多少个？

(2)、王老师在元旦节这天到该体育文化用品商店为学校买篮球和排球各若干个（两种球都买了），商店在他的这笔交易中获利100元王老师有哪几种购买方案．

查看试题解析
21. 已知：△ABC中，BO平分∠ABC，CO平分∠ACB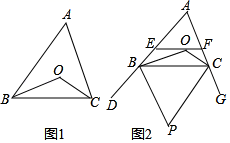

(1)、如图1，∠BOC和∠A有怎样的数量关系？请说明理由

(2)、如图2，过O点的直线分别交△ABC的边AB、AC于E、F（点E不与A，B重合，点F不与A、C重合），BP平分外角∠DBC，CP平分外角∠GCB，BP，CP相交于P．求证：∠P＝∠BOE+∠COF；

(3)、如果（2）中过O点的直线与AB交于E（点E不与A、B重合），与CA的延长线交于F在其它条件不变的情况下，请直接写出∠P、∠BOE、∠COF三个角之间的数量关系．

查看试题解析
22. 如图，直线l₁：y＝x+2与直线l₂：y＝kx+b相交于点P（1，m）

(1)、写出k、b满足的关系；

(2)、如果直线l₂：y＝kx+b与两坐标轴围成一等腰直角三角形，试求直线l₂的函数表达式；

(3)、在（2）的条件下，设直线l₂与x轴相交于点A，点Q是x轴上一动点，求当△APQ是等腰三角形时的Q点的坐标．

查看试题解析

尺码	37	38	39	40	41	42
人数	3	4	4	7	1	1