四川省成都市天府新区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-30 类型:期末考试
一、单选题
-
1. 若 =2,则x的值为( )A、4 B、8 C、﹣4 D、﹣52. 在平面直角坐标系xOy中,点A(-1,-2)关于x轴对称的点的坐标是( )A、(1,2) B、(1,-2) C、(-1,2) D、(-1,-2)3. 下列方程是二元一次方程的是( )A、 B、 、 C、 D、4. 下列各组数是勾股数的是( )A、1,2,3 B、0.3,0.4,0.5 C、6,8,10 D、5,11,125. 下列命题是假命题的是( )A、同角(或等角)的余角相等 B、三角形的任意两边之和大于第三边 C、三角形的内角和为180° D、两直线平行,同旁内角相等6. 估计 +1的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间7. 上体育课时,小明5次投掷实心球的成绩如下表所示,则这组数据的众数与中位数分别是( )
1
2
3
4
5
成绩(m)
8.2
8.0
8.2
7.5
7.8
A、8.2,8.2 B、8.0,8.2 C、8.2,7.8 D、8.2,8.08. 下列图形中,由∠1=∠2,能得到AB∥CD的是( )A、 B、
B、 C、
C、 D、
D、 9. 对于函数y=﹣2x+1,下列结论正确的是( )A、y值随x值的增大而增大 B、它的图象与x轴交点坐标为(0,1) C、它的图象必经过点(﹣1,3) D、它的图象经过第一、二、三象限10. 函数 y=ax﹣a 的大致图象是( )A、
9. 对于函数y=﹣2x+1,下列结论正确的是( )A、y值随x值的增大而增大 B、它的图象与x轴交点坐标为(0,1) C、它的图象必经过点(﹣1,3) D、它的图象经过第一、二、三象限10. 函数 y=ax﹣a 的大致图象是( )A、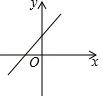 B、
B、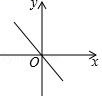 C、
C、 D、
D、
二、填空题
-
11. 点P(﹣3,4)到x轴的距离是 .12. 某公司招聘职员,公司对应聘者进行了面试和笔试(满分均为100分),规定笔试成绩占60%,面试成绩占40%,应聘者张华的笔试成绩和面试成绩分别为95分和90分,她的最终得分是分.13. 已知 是方程组 的解,则5a﹣b的值是 .14. 将一副直角三角板如图摆放,点C在EF上,AC经过点D.已知∠A=∠EDF=90°,AB=AC.∠E=30°,∠BCE=40°,则∠CDF= .
 15. 如图AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,则∠DEG=°.
15. 如图AB∥CD,∠B=72°,EF平分∠BEC,EG⊥EF,则∠DEG=°. 16. 在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,若(a﹣1)2+|b﹣ |+ =0,则这个三角形一定是 .17. 已知一次函数y=kx﹣4(k<0)的图象与两坐标轴所围成的三角形的面积等于8,则该一次函数表达式为 .18. 关于x、y的方程组 与 有相同的解,则a+b的值为 .19. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是 , 点Bn的坐标是 .
16. 在△ABC中,a,b,c分别是∠A,∠B,∠C的对边,若(a﹣1)2+|b﹣ |+ =0,则这个三角形一定是 .17. 已知一次函数y=kx﹣4(k<0)的图象与两坐标轴所围成的三角形的面积等于8,则该一次函数表达式为 .18. 关于x、y的方程组 与 有相同的解,则a+b的值为 .19. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图所示的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则点B3的坐标是 , 点Bn的坐标是 . 20. 定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD= AB,运用:如图2,△ABC中,∠BAC=90°,AB=2,AC=3,点D是BC的中点,将△ABD沿AD翻折得到△AED连接BE,CE,DE,则CE的长为 .
20. 定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD= AB,运用:如图2,△ABC中,∠BAC=90°,AB=2,AC=3,点D是BC的中点,将△ABD沿AD翻折得到△AED连接BE,CE,DE,则CE的长为 .
三、解答题
-
21.(1)、计算:(﹣1)2020+ ﹣|﹣ |+(π﹣2019)0(2)、解方程组:22. △ABC在平面直角坐标系中的位置如图所示,A,B,C三点在格点上.
 (1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、求△A1B1C1的面积.23. 某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
(1)、在图中作出△ABC关于y轴对称的△A1B1C1 .(2)、求△A1B1C1的面积.23. 某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:甲
10
6
10
6
8
乙
7
9
7
8
9
经过计算,甲进球的平均数为8,方差为3.2.
(1)、求乙进球的平均数和方差;(2)、如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?24. 某服装店用4500元购进A,B两种新式服装,按标价售出后可获得毛利润2800元(毛利润=售价一进价),这两种服装的进价、标价如表所示类型价格
A型
B型
进价(元/件)
60
100
标价(元/件)
100
160
(1)、请利用二元一次方程组求A,B两种新式服装各购进的件数;(2)、如果A种服装按标价的9折出售,B种服装按标价的8折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?25. 已知:如图1,在平面直角坐标系中,一次函数y= x+3交x轴于点A,交y轴于点B,点C是点A关于y轴对称的点,过点C作y轴平行的射线CD,交直线AB与点D,点P是射线CD上的一个动点. (1)、求点A,B的坐标.(2)、如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.(3)、若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ , 若存在,请求出对应的点Q坐标;若不存在,请说明理由.26. 九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设 (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为 千米,骑自行车学生骑行的路程为 千米, 关于 的函数图象如图所示.
(1)、求点A,B的坐标.(2)、如图2,将△ACP沿着AP翻折,当点C的对应点C′落在直线AB上时,求点P的坐标.(3)、若直线OP与直线AD有交点,不妨设交点为Q(不与点D重合),连接CQ,是否存在点P,使得S△CPQ=2S△DPQ , 若存在,请求出对应的点Q坐标;若不存在,请说明理由.26. 九年级学生到距离学校6千米的百花公园去春游,一部分学生步行前往,20分钟后另一部分学生骑自行车前往,设 (分钟)为步行前往的学生离开学校所走的时间,步行学生走的路程为 千米,骑自行车学生骑行的路程为 千米, 关于 的函数图象如图所示. (1)、求 关于 的函数解析式;(2)、步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?27. 在等腰Rt△ABC中,AB=AC,∠BAC=90°
(1)、求 关于 的函数解析式;(2)、步行的学生和骑自行车的学生谁先到达百花公园,先到了几分钟?27. 在等腰Rt△ABC中,AB=AC,∠BAC=90° (1)、如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF
(1)、如图1,D,E是等腰Rt△ABC斜边BC上两动点,且∠DAE=45°,将△ABE绕点A逆时针旋转90后,得到△AFC,连接DF①求证:△AED≌△AFD;
②当BE=3,CE=7时,求DE的长;
(2)、如图2,点D是等腰Rt△ABC斜边BC所在直线上的一动点,连接AD,以点A为直角顶点作等腰Rt△ADE,当BD=3,BC=9时,求DE的长.28. 如图,在平面直角坐标系中,直线y=2x+6与x轴交于点A,与y轴交于点B,过点B的直线交x轴于点C,且AB=BC. (1)、求直线BC的解析式;(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);(3)、在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.
(1)、求直线BC的解析式;(2)、点P为线段AB上一点,点Q为线段BC延长线上一点,且AP=CQ,设点Q横坐标为m,求点P的坐标(用含m的式子表示,不要求写出自变量m的取值范围);(3)、在(2)的条件下,点M在y轴负半轴上,且MP=MQ,若∠BQM=45°,求直线PQ的解析式.