四川省成都市龙泉驿区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-30 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，如果点A的坐标为（﹣1，3），那么点A一定在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列各式中正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{1} = 1$ C、 $\sqrt{16} =$ ±4 D、 $\sqrt[3]{9} =$ 3

查看试题解析
3. 在平面直角坐标系中，点A（3，1）关于原点对称的点的坐标是（）

A、（1，3） B、（﹣1，﹣3） C、（﹣3，﹣1） D、（﹣3，1）

查看试题解析
4. 如图，正方形ABCD中，AB=1，则AC的长是（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、2

查看试题解析
5. 关于函数y=2x，下列结论正确的是（）

A、图象经过第一、三象限 B、图象经过第二、四象限 C、图象经过第一、二、三象限 D、图象经过第一、二、四象限

查看试题解析
6. 已知二元一次方程组 ${\begin{array}{l} 2 a + b = 8 \\ 2 a - b = 12 \end{array}$ ，则a的值是（）

A、3 B、5 C、7 D、9

查看试题解析
7. 如图，函数y=ax+b和y=kx的图像交于点P，关于x，y的方程组 ${\begin{array}{l} y - a x = b \\ k x - y = 0 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 3 \end{array}$ B、 ${\begin{array}{l} x = - 3 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = - 3 \\ y = - 2 \end{array}$

查看试题解析
8. 如图，四边形ABCD是菱形，∠ABC＝120°，BD＝4，则BC的长是（）

A、4 B、5 C、6 D、4 $\sqrt{3}$

查看试题解析
9. 正比例函数 $y = k x (k \neq 0)$ 的函数值 $y$ 随 $x$ 的增大而减小，则一次函数的 $y = x - k$ 图象大致是（）

A、 B、 C、 D、

查看试题解析
10. 如图，在矩形ABCD中对角线AC与BD相交于点O，AE⊥BD，垂足为点E，AE=8，AC=20，则OE的长为（）

A、4 $\sqrt{3}$ B、4 C、6 D、8

查看试题解析

二、填空题

11. 比较大小： $\sqrt{6}$ 3(填：“>”或“<”或“=”)

查看试题解析
12. A（3，y₁），B（1，y₂）是直线y=kx+3（k＞0）上的两点，则y₁y₂（填“＞”或“＜）．

查看试题解析
13. 已知（x+y+2）² $+ \sqrt{x - y - 4} =$ 0，则 $\frac{x}{y}$ 的值是．

查看试题解析
14. 如图，在▱ABCD中，对角线AC与BD相交于点O，AC⊥CD，OE∥BC交CD于E，若OC=4，CE=3，则BC的长是．

查看试题解析
15. 求值： $\sqrt{{(\sqrt{5} - 3)}^{2}} =$ ．

查看试题解析
16. 已知关于x，y的方程组 ${\begin{array}{l} 4 x + y = 3 m \\ x - y = 7 m - 5 \end{array}$ 的解满足不等式2x+y＞8，则m的取值范围是．

查看试题解析
17. 如图，在菱形ABCD中，∠BAD=45°，DE是AB边上的高，BE=2，则AB的长是．

查看试题解析
18. 如图，直线y=kx+b与直线y=2x+6关于y轴对称且交于点A，直线y=2x+6交x轴于点B，直线y=kx+b交x轴于点C，正方形DEFG一边DG在线段BC上，点E在线段AB上，点F在线段AC上，则点G的坐标是．

查看试题解析
19. 如图，在矩形ABCD中，AB=3，点E为边CD上一点，将△ADE沿AE所在直线翻折，得到△AFE，点F恰好是BC的中点，M为AF上一动点，作MN⊥AD于N，则BM+AN的最小值为．

查看试题解析

三、解答题

20. 计算

(1)、2 $\sqrt{18} -$ 6 $\times \sqrt{\frac{1}{2}} + \sqrt[3]{27}$

(2)、（ $\sqrt{5} -$ 2）²﹣（ $\sqrt{13} -$ 2）（ $\sqrt{13} +$ 2）

查看试题解析
21. 解方程组

(1)、 ${\begin{array}{l} x - 2 y = 0 ① \\ 3 x + 5 y = - 22 ② \end{array}$

(2)、 ${\begin{array}{l} 2 x - 3 y = 0 ① \\ 3 x + y = 5 ② \end{array}$

查看试题解析
22. 如图，在 $▱$ ABCD中，点E，F分别在BC，AD上，且BE=FD，求证：四边形AECF是平行四边形．

查看试题解析
23. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 3 x + 2 y = 8 m + 20 ① \\ x + 2 y = 6 m ② \end{array}$ 的解满足x=y，求m的值．

查看试题解析
24. 如图，在平面直角坐标系中，直线l₁：y=x+6与y轴交于点A，直线l₂：y=kx+b与y轴交于点B，与l₁相交于C（﹣3，3），AO=2BO．

(1)、求直线l₂：y=kx+b的解析式；

(2)、求△ABC的面积．

查看试题解析
25. 如图1，已知矩形ABCD，连接AC，将△ABC沿AC所在直线翻折，得到△AEC，AE交CD于点F．

(1)、求证：DF=EF；

(2)、如图2，若∠BAC=30°，点G是AC的中点，连接DE，EG，求证：四边形ADEG是菱形．

查看试题解析
26. A，B两地相距80km，甲、乙两人骑车同时分别从A，B两地相向而行，假设他们都保持匀速行驶，则他们各自到A地的距离s（km）都是骑车时间t（h）的一次函数，如图所示．

(1)、求乙的s_乙与t之间的解析式；

(2)、经过多长时间甲乙两人相距10km？

查看试题解析
27. 如图，已知正方形ABCD，AB=8，点E是射线DC上一个动点（点E与点D不重合），连接AE，BE，以BE为边在线段AD的右侧作正方形BEFG，连结CG．

(1)、当点E在线段DC上时，求证：△BAE≌△BCG；

(2)、在（1）的条件下，若CE=2，求CG的长；

(3)、连接CF，当△CFG为等腰三角形时，求DE的长．

查看试题解析
28. 如图，直线y=﹣2x+8分别交x轴，y轴于点A ， B ，直线y $= \frac{1}{2}$ x+3交y轴于点C ，两直线相交于点D ．

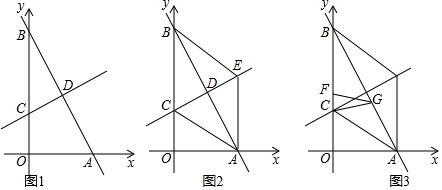(1)、求点D的坐标；

(2)、如图2，过点A作AE∥y轴交直线y $= \frac{1}{2}$ x+3于点E ，连接AC ， BE ．求证：四边形ACBE是菱形；

(3)、如图3，在（2）的条件下，点F在线段BC上，点G在线段AB上，连接CG ， FG ，当CG=FG ，且∠CGF=∠ABC时，求点G的坐标．

查看试题解析