四川省成都市金牛区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-30 类型:期末考试
一、单选题
-
1. 在实数中 , , , 是无理数的是( )A、 B、 C、 D、2. 点P(-2,-3)关于x轴的对称点为( )A、 B、 C、 D、3. 下面各组数中不能构成直角三角形三边长的一组数是( )A、 B、 C、 D、4. 在关于 的函数, 中,自变量 的取值范围是( )A、 B、 C、 D、5. 已知 ,则下列不等式中正确的是( )A、 B、 C、 D、6. 下列四个命题中,真命题有( )
①两条直线被第三条直线所截,内错角相等.
②如果 ,那么 与 是对顶角.
③三角形的一个内角大于任何一个外角.
④如果 ,那么 .
A、 个 B、 个 C、 个 D、 个7. 一次函数 的图象不经过的象限是( )A、一 B、二 C、三 D、四8. 已知点 , 都在直线 上,则 , 的值的大小关系是( )A、 B、 C、 D、不能确定9. 已知方程组 中的 , 互为相反数,则 的值为( )A、 B、 C、 D、10. A,B两地相距20 ,甲乙两人沿同一条路线从 地到 地,如图反映的是二人行进路程 ( )与行进时间 ( )之间的关系,有下列说法:①甲始终是匀速行进,乙的行进不是匀速的;②乙用了4个小时到达目的地;③乙比甲先出发1小时;④甲在出发4小时后被乙追上,在这些说法中,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
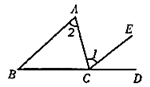
11. 满足 的整数 的值 .12. 若一个正比例函数的图象经过 、 )两点,则 的值为 .13. 如图,已知 , 则 .
 14. 如图,由两个直角三角形和三个正方形组成的图形,已知 , 其中阴影部分面积是平方单位.
14. 如图,由两个直角三角形和三个正方形组成的图形,已知 , 其中阴影部分面积是平方单位. 15. 已知 、 ,满足 ,则 的平方根为 .16. 关于 , 的二元一次方程组 的解是 ,如图,在平面直角坐标系 中,直线 与直线 相交于点 ,则点 的坐标为.
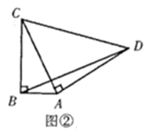
15. 已知 、 ,满足 ,则 的平方根为 .16. 关于 , 的二元一次方程组 的解是 ,如图,在平面直角坐标系 中,直线 与直线 相交于点 ,则点 的坐标为. 17. 若关于 的不等式组 有且只有五个整数解,则 的取值范围是.18. 如图,在 中, , , ,点 在 上,将 沿 折叠,点 落在点 处, 与 相交于点 ,若 ,则 的长是.
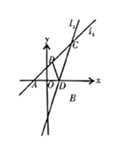
17. 若关于 的不等式组 有且只有五个整数解,则 的取值范围是.18. 如图,在 中, , , ,点 在 上,将 沿 折叠,点 落在点 处, 与 相交于点 ,若 ,则 的长是.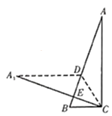 19. 如图,直线 与 轴正方向夹角为 ,点 在 轴上,点 在直线 上, 均为等边三角形,则 的横坐标为 .
19. 如图,直线 与 轴正方向夹角为 ,点 在 轴上,点 在直线 上, 均为等边三角形,则 的横坐标为 .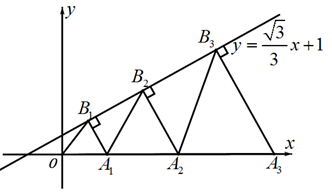
三、解答题
-
20. 计算:(1)、(2)、21. 解方程组或不等式组:(1)、(2)、解不等式组 ,并把解集在数轴上表示出来.
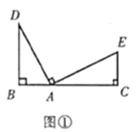
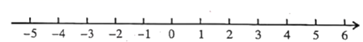 22. 如图,直线 分别交 和 于点 、 ,点 在 上, ,且 .求证: .
22. 如图,直线 分别交 和 于点 、 ,点 在 上, ,且 .求证: .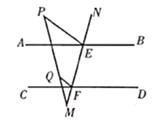 23. 某市为了鼓励居民节约用水,决定水费实行两级收费制度.若每月用水量不超过10吨(含10吨),则每吨按优惠价m元收费;若每月用水量超过10吨,则超过部分每吨按市场价 元收费,小明家3月份用水20吨,交水费50元;4月份用水18吨,交水费44元.(1)、求每吨水的优惠价和市场价分别是多少?(2)、设每月用水量为 吨,应交水费为 元,请写出 与 之间的函数关系式.24. 某校在八年级开展环保知识问卷调查活动,问卷一共10道题,每题10分,八年级(三)班的问卷得分情况统计图如下图所示:
23. 某市为了鼓励居民节约用水,决定水费实行两级收费制度.若每月用水量不超过10吨(含10吨),则每吨按优惠价m元收费;若每月用水量超过10吨,则超过部分每吨按市场价 元收费,小明家3月份用水20吨,交水费50元;4月份用水18吨,交水费44元.(1)、求每吨水的优惠价和市场价分别是多少?(2)、设每月用水量为 吨,应交水费为 元,请写出 与 之间的函数关系式.24. 某校在八年级开展环保知识问卷调查活动,问卷一共10道题,每题10分,八年级(三)班的问卷得分情况统计图如下图所示: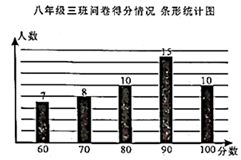 (1)、扇形统计图中,a的值为 .(2)、根据以上统计图中的信息,求这问卷得分的众数和中位数分别是多少分?(3)、已知该校八年级共有学生600人,请估计问卷得分在80分以上(含80分)的学生约有多少人?25. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与 轴交于点 ,与直线 相交于点 ,
(1)、扇形统计图中,a的值为 .(2)、根据以上统计图中的信息,求这问卷得分的众数和中位数分别是多少分?(3)、已知该校八年级共有学生600人,请估计问卷得分在80分以上(含80分)的学生约有多少人?25. 如图,在平面直角坐标系 中,直线 与 轴交于点 ,与 轴交于点 ,与直线 相交于点 , (1)、求直线 的函数表达式;(2)、求 的面积;(3)、在 轴上是否存在一点 ,使 是等腰三角形.若不存在,请说明理由;若存在,请直接写出点 的坐标26. 甲乙两人同时登同一座山,甲乙两人距地面的高度 (米)与登山时间 (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、在 轴上是否存在一点 ,使 是等腰三角形.若不存在,请说明理由;若存在,请直接写出点 的坐标26. 甲乙两人同时登同一座山,甲乙两人距地面的高度 (米)与登山时间 (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: (1)、乙在提速前登山的速度是米/分钟,乙在 地提速时距地面的高度 为米.(2)、若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后 和 之间的函数关系式.(3)、登山多长时间时,乙追上了甲,此时甲距 地的高度为多少米?
(1)、乙在提速前登山的速度是米/分钟,乙在 地提速时距地面的高度 为米.(2)、若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后 和 之间的函数关系式.(3)、登山多长时间时,乙追上了甲,此时甲距 地的高度为多少米?