四川省成都市成华区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-29 类型：期末考试

进入出卷网下载

一、单选题

1. 在实数0，﹣ $\sqrt{2}$ ，π，|﹣3|中，最小的数是（）

A、0 B、﹣ $\sqrt{2}$ C、π D、|﹣3|

查看试题解析
2. 化简 $\sqrt{12}$ 的结果是（　　）

A、 $4 \sqrt{3}$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{2}$ D、 $2 \sqrt{6}$

查看试题解析
3. 如图，直线 $a / / b$ ，直线 $A B ⊥ A C$ ，若 $∠ 1 = 50^{\circ}$ ，则 $∠ 2 =$ （）

A、 $50^{\circ}$ B、 $45^{\circ}$ C、 $40^{\circ}$ D、 $30^{\circ}$

查看试题解析
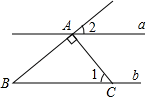4. 估计 $\sqrt{33}$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
5. 平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标为（　　）

A、（﹣2，﹣3） B、（2，﹣3） C、（﹣3，﹣2） D、（3，﹣2）

查看试题解析
6. 如果直线y＝kx+b经过一、二、四象限，则有（）

A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
7. 满足下列条件的△ABC不是直角三角形的是（）

A、AC＝1，BC＝ $\sqrt{3}$ ，AB＝2 B、AC：BC：AB＝3：4：5 C、∠A：∠B：∠C＝1：2：3 D、∠A：∠B：∠C＝3：4：5

查看试题解析
8. 某次知识竞赛共有20道题，规定：每答对一道题得＋5分，每答错一道题得－2分，不答的题得0分．已知圆圆这次竞赛得了60分，设圆圆答对了x道题，答错了y道题，则（）

A、x－y＝20 B、x＋y＝20 C、5x－2y＝60 D、5x＋2y＝60

查看试题解析
9. 在平面直角坐标系中，将函数 $y = 3 x$ 的图象向上平移6个单位长度，则平移后的图象与x轴的交点坐标为（）

A、(2,0) B、(-2,0) C、(6,0) D、(-6,0)

查看试题解析
10. 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

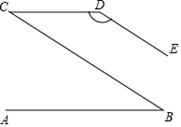
11. 使 $\sqrt{x - 3}$ 有意义的x的取值范围是.

查看试题解析
12. 如图，AB∥CD ， DE∥CB ， ∠B＝35°，则∠D＝°．

查看试题解析
13. 从甲、乙、丙三人中选一人参加环保知识抢答赛，经过两轮初赛，他们的平均成绩都是89.7，方差分别是 $S_{甲}^{2} = 2.83, S_{乙}^{2} = 1 .71, S_{丙}^{2} = 3 .52,$ 你认为适合参加决赛的选手是．

查看试题解析
14. 如图，在△ABC中，∠A＝70°．按下列步骤作图：①分别以点B，C为圆心，适当长为半径画弧，分别交BA，BC，CA，CB于点D，E，F，G；②分别以点D，E为圆心，大于 $\frac{1}{2}$ DE为半径画弧，两弧交于点M；③分别以点F，G为圆心，大于 $\frac{1}{2}$ FG为半径画弧，两弧交于点N；④作射线BM交射线CN于点O．则∠BOC的度数是．

查看试题解析
15. 若 $\sqrt{x + 2}$ +（y﹣1）²＝0，则（x+y）²⁰²⁰＝．

查看试题解析
16. 若a﹣b+6的算术平方根是2，2a+b﹣1的平方根是±4，则a﹣5b+3的立方根是.

查看试题解析
17. 七巧板被誉为“东方魔板”．小明利用七巧板（如图1）中各板块的边长之间的关系拼成一个凸六边形，则该凸六边形（如图2）的周长是．

查看试题解析
18. 在8×8的格子纸上，1×1小方格的顶点叫做格点．△ABC 的三个顶点都是格点（位置如图）．若一个格点P使得△PBC与△PAC的面积相等，就称P点为“好点”．那么在这张格子纸上共有个“好点”．

查看试题解析
19. 如图，直线y＝2x﹣1分别交x，y轴于点A，B，点C在x轴的正半轴，且∠ABC＝45°，则直线BC的函数表达式是．

查看试题解析

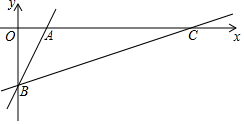
三、解答题

20.

(1)、计算： $\frac{9}{2} \sqrt{\frac{1}{3}} + \frac{1}{2} \sqrt{48} - \sqrt{\frac{75}{4}}$

(2)、计算： $\sqrt{{(- 2)}^{2}} \times \frac{1}{2} - \sqrt{3^{2}} + \sqrt{\frac{4}{9}} \div \frac{1}{3}$

查看试题解析
21.

(1)、解方程组： ${\begin{array}{l} 3 x + 2 y = 0 (1) \\ 2 x - 3 y = 13 (2) \end{array}$

(2)、解方程组： ${\begin{array}{l} x - y - 1 = 0 (1) \\ 4 (x - y) - y = 5 (2) \end{array}$

查看试题解析
22. 本学期初，某校为迎接中华人民共和国成立七十周年，开展了以“不忘初心，缅怀革命先烈，奋斗新时代“为主题的读书活动．德育处对八年级学生九月份“阅读该主题相关书籍的读书量”（下面简称：“读书量”）进行了随机抽样调查，并对所有随机抽取学生的“读书量”（单位：本）进行了统计，绘制了两幅不完整的统计图（如图所示）．

(1)、请补全两幅统计图；本次所抽取学生九月份“读书量“的众数是多少；

(2)、求本次所抽取学生九月份“读书量”的平均数；

(3)、已知该校八年级有500名学生，请你估计该校八年级学生中，九月份“读书量“为5本的学生人数．

查看试题解析
23. 若买3根跳绳和6个毽子共72元；买1根跳绳和5个毽子共36元．

(1)、跳绳、毽子的单价各是多少元？

(2)、元旦促销期间，所有商品按同样的折数打折销售，买10根跳绳和10个毽子只需180元，问商品按原价的几折销售？

查看试题解析
24. 如图，一次函数y＝kx+b的图象经过点A （﹣2，6），与x轴交于点B，与正比例函数y＝3x的图象交于点C，点C的横坐标为1．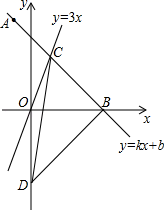

(1)、求AB的函数表达式；

(2)、若点D在y轴负半轴，且满足S_△_COD＝ $\frac{1}{3}$ S_△_BOC ，求点D的坐标．

查看试题解析
25. 我们定义：对角线互相垂直的四边形叫做垂美四边形．

(1)、如图1，垂美四边形ABCD的对角线AC，BD交于O．求证：AB²+CD²＝AD²+BC²；

(2)、如图2，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE，连结BE，CG，GE．
①求证：四边形BCGE是垂美四边形；

②若AC＝4，AB＝5，求GE的长．

查看试题解析
26. 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案．
甲公司方案：每月的养护费用y（元）与绿化面积x（平方米）是一次函数关系，如图所示．
乙公司方案：绿化面积不超过1000平方米时，每月收取费用5500 元；绿化面积超过1000平方米时，每月在收取5500元的基础上，超过部分每平方米收取4元．

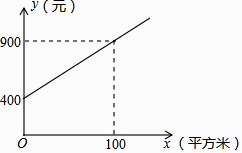(1)、求如图所示的y与x的函数解析式：（不要求写出定义域）；

(2)、如果某学校目前的绿化面积是1200平方米，试通过计算说明：选择哪家公司的服务，每月的绿化养护费用较少．

查看试题解析
27. 在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．过射线AD上一点M作BM的垂线，交直线AC于点N．

(1)、如图1，点M在AD上，若∠N＝15°，BC＝2 $\sqrt{3}$ ，则线段AM的长为；

(2)、如图2，点M在AD上，求证：BM＝NM；

(3)、若点M在AD的延长线上，则AB，AM，AN之间有何数量关系？直接写出你的结论，不证明．

查看试题解析
28. 定义：在平面直角坐标系中，对于任意两点A （a，b），B（c，d），若点T（x，y）满足x＝ $\frac{a + c}{3}$ ，y＝ $\frac{b + d}{3}$ ，那么称点T是点A和B的融合点．例如：M（﹣1，8），N（4，﹣2），则点T（1，2）是点M和N的融合点．如图，已知点D（3，0），点E是直线y＝x+2上任意一点，点T （x，y）是点D和E的融合点．

(1)、若点E的纵坐标是6，则点T的坐标为；

(2)、求点T （x，y）的纵坐标y与横坐标x的函数关系式：

(3)、若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标．

查看试题解析