湖南省长沙市开福区青竹湖湘一外国语学2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-29 类型：期末考试

进入出卷网下载

一、单选题

1. 我国民间，流传着许多含有吉祥意义的图案，表示对幸福生活的向往，良辰佳节的祝贺.比如下列图案分别表示“福”“禄”“寿”“喜”，其中是轴对称图形的有几个（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 如果把分式 $\frac{x + y}{x y}$ 中的x，y同时扩大为原来的4倍，现么该分式的值（）

A、不变 B、扩大为原来的4倍 C、缩小为原来的 $\frac{1}{2}$ D、缩小为原来的 $\frac{1}{4}$

查看试题解析
3. 生物学家发现了一种病毒，其长度约为0.0000000052mm，数据0.0000000052用科学记数法表示正确的是（）

A、 $5.2 \times 10^{8}$ B、 $5.2 \times 10^{9}$ C、 $5.2 \times 10^{- 9}$ D、 $5.2 \times 10^{- 8}$

查看试题解析
4. 下面命题的逆命题正确的是（）

A、对顶角相等 B、邻补角互补 C、矩形的对角线互相平分 D、等腰三角形两腰相等

查看试题解析
5. 已知x﹣y＝﹣2，xy＝3，则x²y﹣xy²的值为（）

A、2 B、﹣6 C、5 D、﹣3

查看试题解析
6. 小明上月在某文具店正好用20元钱买了几本笔记本，本月再去买时，恰遇此文具店搞优惠酬宾活动，同样的笔记本，每本比上月便宜1元，结果小明只比上次多用了4元钱，却比上次多买了2本．若设他上月买了x本笔记本，则根据题意可列方程（　　）

A、 $\frac{24}{x + 2} - \frac{20}{x}$ =1 B、 $\frac{20}{x} - \frac{24}{x + 2}$ =1 C、 $\frac{24}{x} - \frac{20}{x + 2}$ =1 D、 $\frac{20}{x + 2} - \frac{24}{x}$ =1

查看试题解析
7. 若 $\sqrt{{(4 - a)}^{2}} = a - 4$ ，则a与4的大小关系是（）

A、a＝4 B、a＞4 C、a≤4 D、a≥4

查看试题解析
8. 下列各组线段中，能够组成直角三角形的一组是（）

A、1，2，3 B、2，3，4 C、4，5，6 D、1， $\sqrt{3}$ ，2

查看试题解析
9. 如图，△ABC中，AB＝AC，DE垂直平分AC，若△BCD的周长是14，BC＝6，则AC的长是（）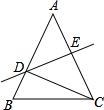

A、6 B、8 C、10 D、14

查看试题解析
10. 如图，O是矩形ABCD对角线AC的中点，M是AD的中点，若BC＝8，OB＝5，则OM的长为（）

A、1 B、2 C、3 D、4

查看试题解析
11. 下列调查适合抽样调查的是（）

A、审核书稿中的错别字 B、企业招聘，对应聘人员进行面试 C、了解八名同学的视力情况 D、调查某批次汽车的抗撞击能力

查看试题解析
12. 在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m．其行走路线如图所示，第1次移动到A₁ ，第2次移动到A₂ ， …第n次移动到A_n ．则△OA₆A₂₀₂₀的面积是（）

A、505 $m^{2}$ B、504.5 $m^{2}$ C、505.5 $m^{2}$ D、1010 $m^{2}$

查看试题解析

二、填空题

13. 分解因式2m²﹣32＝．

查看试题解析
14. 若分式 $\frac{| x | - 3}{3 + x}$ 的值是0，则x的值为．

查看试题解析
15. 若式子 $\sqrt{2 x - 1}$ 在实数范围内有意义，则x应满足的条件是．

查看试题解析
16. 如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形，若正方形A、B、C、E的面积分别为2，5，1，10．则正方形D的面积是．

查看试题解析
17. 某中学为了解学生上学方式，现随机抽取部分学生进行调查，将结果绘成如图所示的条形图，由此可估计该校2000名学生有名学生是骑车上学的．

查看试题解析
18. △ABC与△DEF是两个全等的等腰直角三角形，∠BAC=∠D=90°，AB=AC= $\sqrt{6}$ ．现将△DEF与△ABC按如图所示的方式叠放在一起，使△ABC保持不动，△DEF运动，且满足点E在边BC上运动（不与B，C重合），边DE始终经过点A，EF与AC交于点M．在△DEF运动过程中，若△AEM能构成等腰三角形，则BE的长为．

查看试题解析

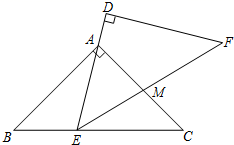
三、解答题

19. 计算： $2 \sqrt{18} + {(π - 2020)}^{0} - {(- \frac{1}{2})}^{- 2} + \sqrt{{(\sqrt{2} - 1)}^{2}}$ ．

查看试题解析
20. 先化简，再求值： $\frac{a^{2} - 1}{a^{2} - a}$ ÷（2+ $\frac{a^{2} + 1}{a}$ ），其中a＝ $\sqrt{2}$ ﹣2．

查看试题解析
21. 已知在平面直角坐标系中有三点A（﹣2，1），B（3，1），C（2，3），请解答下列问题：

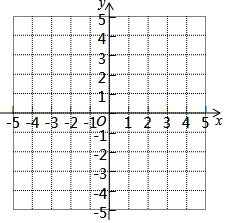(1)、在坐标系内描出A，B，C的位置；

(2)、画出△ABC关于x轴对称的图形△A₁B₁C₁ ，并写出顶点A₁ ， B₁ ， C₁的坐标；

(3)、写出∠C的度数．

查看试题解析
22. 如图，在平行四边形ABCD中，点E为AD的中点，延长CE交BA的延长线于点F．

(1)、求证：AB＝AF；

(2)、若BC＝2AB，∠BCD＝100°，求∠ABE的度数．

查看试题解析
23. 雾霾天气持续笼罩我国大部分地区，困扰着广大市民的生活，口罩市场出现热销，小明的爸爸用12000元购进甲、乙两种型号的口罩在自家商店销售，销售完后共获利2700元，进价和售价如表：

(1)、小明爸爸的商店购进甲、乙两种型号口罩各多少袋？

(2)、该商店第二次以原价购进甲、乙两种型号口罩，购进甲种型号口罩袋数不变，而购进乙种型号口罩袋数是第一次的2倍，甲种口罩按原售价出售，而效果更好的乙种口罩打折让利销售，若两种型号的口罩全部售完，要使第二次销售活动获利不少于2460元，每袋乙种型号的口罩最多打几折？

查看试题解析
24. 已知：如图，在矩形ABCD中，AB＝6，BC＝8，E为直线BC上一点．

(1)、如图1，当E在线段BC上，且DE＝AD时，求BE的长；

(2)、如图2，点E为BC延长长线上一点，若BD＝BE，连接DE，M为ED的中点，连接AM，CM，求证：AM⊥CM；

(3)、如图3，在（2）条件下，P，Q为AD边上的两个动点，且PQ＝5，连接PB、MQ、BM，求四边形PBMQ的周长的最小值．

查看试题解析
25. 我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= $\frac{p}{q}$ ．
例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= $\frac{3}{4}$ ．

(1)、如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
求证：对任意一个完全平方数m，总有F（m）=1；

(2)、如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；

(3)、在（2）所得“吉祥数”中，求F（t）的最大值．

查看试题解析
26. 在平面直角坐标中，四边形OCNM为矩形，如图1，M点坐标为（m，0），C点坐标为（0，n），已知m，n满足 $\sqrt{n - 5} + | 5 - m | = 0$ ．

(1)、求m，n的值；

(2)、①如图1，P，Q分别为OM，MN上一点，若∠PCQ＝45°，求证：PQ＝OP+NQ；
②如图2，S，G，R，H分别为OC，OM，MN，NC上一点，SR，HG交于点D．若∠SDG＝135°， $HG = \frac{5 \sqrt{5}}{2}$ ，求RS的长；

(3)、如图3，在矩形OABC中，OA＝5，OC＝3，点F在边BC上且OF＝OA，连接AF，动点P在线段OF是（动点P与O，F不重合），动点Q在线段OA的延长线上，且AQ＝FP，连接PQ交AF于点N，作PM⊥AF于M．试问：当P，Q在移动过程中，线段MN的长度是否发生变化？若不变求出线段MN的长度；若变化，请说明理由．

查看试题解析