湖南省张家界市慈利县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-29 类型:期末考试
一、填空题
-
1. 要使分式 的值存在,则 的取值应满足( )A、 B、 C、 D、2. 下列约分正确的是( )A、 B、 C、 D、3. 下列各组线段,能构成三角形的是( )A、 B、 C、 D、4. 如图所示,小明书上的三角形被墨水污染了,他根据所学知识画出了完全一样的一个三角形,他根据的定理是( )
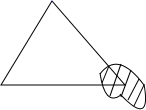 A、SSS B、SAS C、AAS D、ASA5. 在实数 , ,3.1415926, 1.010010001…(相邻两个1之间逐次加一个0), , 中,无理数有( )A、1个 B、2个 C、3个 D、4个6. 不等式组 的解集在数轴上表示正确的是( )A、
A、SSS B、SAS C、AAS D、ASA5. 在实数 , ,3.1415926, 1.010010001…(相邻两个1之间逐次加一个0), , 中,无理数有( )A、1个 B、2个 C、3个 D、4个6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、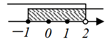 C、
C、 D、
D、 7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,点E、F、C、B在同一直线上,AB=DE,∠A=∠D,添加下列一个条件,不能判定△ABC≌△DEF的条件是( )
7. 下列运算正确的是( )A、 B、 C、 D、8. 如图,点E、F、C、B在同一直线上,AB=DE,∠A=∠D,添加下列一个条件,不能判定△ABC≌△DEF的条件是( ) A、∠ACB=∠DFE B、AC=DE C、∠B=∠E D、BC=EF
A、∠ACB=∠DFE B、AC=DE C、∠B=∠E D、BC=EF二、填空题
-
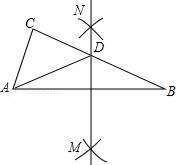
9. 若分式 的值为0,则 的值为.10. 如图,在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于点M,N,作直线MN,交BC于点D,连接AD.若△ADC的周长为10,AB=7,则△ABC的周长为 .
 11. 若分式方程 有增根,则m的值是12. 已知 的平方根是 ,则 的立方根是.13. 已知实数a在数轴上的位置如图所示,则化简|a-1|- 的结果是.
11. 若分式方程 有增根,则m的值是12. 已知 的平方根是 ,则 的立方根是.13. 已知实数a在数轴上的位置如图所示,则化简|a-1|- 的结果是.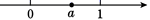 14. 不等式组 的解集为x>2,则a的取值范围是 .15. 如图,△ABC中,∠ABC=50° , ∠ACB=70° , AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= .
14. 不等式组 的解集为x>2,则a的取值范围是 .15. 如图,△ABC中,∠ABC=50° , ∠ACB=70° , AD平分线∠BAC.过点D作DE⊥AB于点E,则∠ADE= .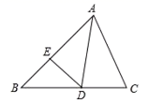 16. 如图,点A,A1 , A2 , A3 , …在同一直线上,AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4 , …,若∠B的度数为 ,则∠A2019A2020B2019的度数为 .
16. 如图,点A,A1 , A2 , A3 , …在同一直线上,AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4 , …,若∠B的度数为 ,则∠A2019A2020B2019的度数为 .
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 。19. 解一元一次不等式组 并写出它的整数解.20. 某校为了丰富学生的校园生活,准备购进一批篮球和足球,其中篮球的单价比足球的单价多40元,用1500元购进的篮球个数与900元购进的足球个数相同,篮球与足球的单价各是多少元?
21. 计算:(1)、(2)、22. 雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE= AB,AF= AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.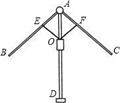 23. 阅读下列解题过程:
23. 阅读下列解题过程:…
(1)、化简:(2)、观察上面的解题过程,请你猜想一规律:直接写出式子 ;(3)、利用这一规律计算: 的值24. 如图(1),AB=7cm,AC⊥AB,BD⊥AB 垂足分别为 A、B,AC=5cm.点P 在线段 AB 上以 2cm/s 的速度由点 A 向点B 运动,同时,点 Q 在射线 BD 上运动.它们运 动的时间为 t(s)(当点 P 运动结束时,点 Q 运动随之结束). (1)、若点 Q 的运动速度与点 P 的运动速度相等,当 t=1 时,△ACP 与△BPQ 是否全等, 并判断此时线段 PC 和线段 PQ 的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB” 改为 “∠CAB=∠DBA=60°”,点 Q 的运动速 度为 x cm/s,其他条件不变,当点 P、Q 运动到某处时,有△ACP 与△BPQ 全等,求出相应的 x、t 的值.
(1)、若点 Q 的运动速度与点 P 的运动速度相等,当 t=1 时,△ACP 与△BPQ 是否全等, 并判断此时线段 PC 和线段 PQ 的位置关系,请分别说明理由;(2)、如图(2),若“AC⊥AB,BD⊥AB” 改为 “∠CAB=∠DBA=60°”,点 Q 的运动速 度为 x cm/s,其他条件不变,当点 P、Q 运动到某处时,有△ACP 与△BPQ 全等,求出相应的 x、t 的值.