湖南省岳阳市平江县2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-29 类型:期末考试
一、单选题
-
1. 如果分式 在实数范围内有意义,则 的取值范围是( )A、 B、 C、全体实数 D、2. 在 , , , , , ,等五个数中,无理数有( )A、 个 B、 个 C、 个 D、 个3. 下列命题是假命题的是( )A、有一个外角是120°的等腰三角形是等边三角形 B、等边三角形有3条对称轴 C、有两边和一角对应相等的两个三角形全等 D、有一边对应相等的两个等边三角形全等4. 下列二次根式中,最简二次根式的是( )A、 B、 C、 D、5. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为( )A、 B、 C、 D、6. 下列说法正确的是( )A、 的平方根是 B、 的算术平方根是 C、 的立方根是 D、 是 的一个平方根7. 等腰三角形的顶角为150°,则它的底角为( )A、30° B、15° C、30°或15° D、50°8. 如图,在△ABC中,AB=AC,点D,E在BC上,连接AD,AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
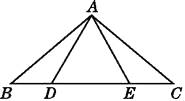 A、BD=CE B、AD=AE C、DA=DE D、BE=CD
A、BD=CE B、AD=AE C、DA=DE D、BE=CD二、填空题
-
9. 已知一粒米的质量是0.000021千克,这个数字用科学记数法表示为.10. 一根木棒能与长为 和 的两根木棒钉成一个三角形,则这根木棒的长度 的取值范围是.11. 若二次根式 在实数范围内有意义,则 的取值范围是 .12.
如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为
 13. 如图所示的数轴上,点 与点 关于点 对称, 、 两点对应的实数是 和 ,则线段 的长为 .
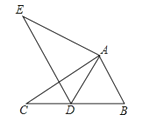
13. 如图所示的数轴上,点 与点 关于点 对称, 、 两点对应的实数是 和 ,则线段 的长为 .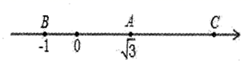 14. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .15. 计算: .16. 如图, 是 的中线, 、 分别是 和 延长线上的点,且 ,连接 、 ,下列说法:① 和 的面积相等,② ,③ ,④ ,⑤ ,其中一定正确的答案有 . (只填写正确的序号)
14. 当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的“特征角”为100°,那么这个“特征三角形”的最小内角的度数为 .15. 计算: .16. 如图, 是 的中线, 、 分别是 和 延长线上的点,且 ,连接 、 ,下列说法:① 和 的面积相等,② ,③ ,④ ,⑤ ,其中一定正确的答案有 . (只填写正确的序号)
三、解答题
-
17. 计算:18. 解方程:19. 化简分式 ,并在0、1、-1、2、-2中选一个你喜欢的数作为a的值,求代数式的值20. 解不等式组: ,并将解集在数轴上表示出来.
 21. 如图, , , 的垂直平分线交 于 ,
21. 如图, , , 的垂直平分线交 于 , (1)、求 的度数;(2)、若 , ,求 的周长.22. “绿水青山就是金山银山”,随着生活水平的提高人们对饮水品质的需求越来越高,岳阳市槐荫公司根据市场需求代理 , 两种型号的净水器,每台 型净水器比每台 型净水器进价多 元,用 万元购进 型净水器与用 万元购进 型净水器的数量相等(1)、求每台 型、 型净水器的进价各是多少元?(2)、槐荫公司计划购进 , 两种型号的共 台进行试销,购买资金不超过 万元.试求最多可以购买 型净水器多少台?23. 描述证明:
(1)、求 的度数;(2)、若 , ,求 的周长.22. “绿水青山就是金山银山”,随着生活水平的提高人们对饮水品质的需求越来越高,岳阳市槐荫公司根据市场需求代理 , 两种型号的净水器,每台 型净水器比每台 型净水器进价多 元,用 万元购进 型净水器与用 万元购进 型净水器的数量相等(1)、求每台 型、 型净水器的进价各是多少元?(2)、槐荫公司计划购进 , 两种型号的共 台进行试销,购买资金不超过 万元.试求最多可以购买 型净水器多少台?23. 描述证明:小明在研究数学问题时发现了一个有趣的现象:
 (1)、请你用数学表达式补充完整小明发现的这个有趣的现象;(2)、请你证明小明发现的这个有趣现象.24. 如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)、请你用数学表达式补充完整小明发现的这个有趣的现象;(2)、请你证明小明发现的这个有趣现象.24. 如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转. (1)、如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想.(2)、若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(1)、如图2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想.(2)、若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.