湖南省益阳市赫山区2019-2020学年八年级上学期数学期末试卷
试卷更新日期:2020-12-29 类型:期末考试
一、单选题
-
1. 3的平方根是( )A、 B、 C、 D、32. 若 ,则下列不等式正确的是( )A、 B、 C、 D、3. 若分式 的值为0,则x应满足的条件是( )A、x = -1 B、x ≠ -1 C、x = ±1 D、x = 14. 把分式 约分得( )A、 B、 C、 D、5. 已知三角形三边长3,4, ,则 的取值范围是( )A、 B、 C、 D、6. 如图所示,小琳总结了“解可化为一元一次方程的分式方程”的运算流程,那么A和B分别代表的是( )
 A、分式的基本性质,最简公分母 B、分式的基本性质,最简公分母 C、等式的基本性质2,最简公分母 D、等式的基本性质2,最简公分母7. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( )
A、分式的基本性质,最简公分母 B、分式的基本性质,最简公分母 C、等式的基本性质2,最简公分母 D、等式的基本性质2,最简公分母7. 如图,以点O为圆心,任意长为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画出射线OB,则∠AOB=( ) A、30° B、45° C、60° D、90°8. 等式 成立的x的取值范围在数轴上可表示为( )A、
A、30° B、45° C、60° D、90°8. 等式 成立的x的取值范围在数轴上可表示为( )A、 B、
B、 C、
C、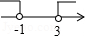 D、
D、 9. 下列运算正确的是( )A、 B、 C、 D、10. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则a可以是( )
9. 下列运算正确的是( )A、 B、 C、 D、10. 如图是一个2×2的方阵,其中每行、每列的两数和相等,则a可以是( ) A、-2 B、 C、0 D、
A、-2 B、 C、0 D、二、填空题
-
11. 华为Mate20手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为 .12. 若 在实数范围内有意义,则 的取值范围是.13. 已知 ,且 , 为两个连续的整数,则 .14. 如图, 中, 、 的平分线交于 点, ,则 .
 15. 若不等式组 的解集是 ,则m的取值范围是 .16. 某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,设原来每天生产汽车 辆,则列出的不等式为 .17. 在学习平方根的过程中,同学们总结出:在 中,已知底数 和指数 ,求幂 的运算是乘方运算:已知幂 和指数 ,求底数 的运算是开方运算.小明提出一个问题: “如果已知底数 和幕 ,求指数 是否也对应着一种运算呢?”老师首先肯定了小明善于思考,继而告诉大家这是同学们进入高中将继续学习的对数,感兴趣的同学可以课下自主探究.
15. 若不等式组 的解集是 ,则m的取值范围是 .16. 某汽车厂改进生产工艺后,每天生产的汽车比原来每天生产的汽车多6辆,那么现在15天的产量就超过了原来20天的产量,设原来每天生产汽车 辆,则列出的不等式为 .17. 在学习平方根的过程中,同学们总结出:在 中,已知底数 和指数 ,求幂 的运算是乘方运算:已知幂 和指数 ,求底数 的运算是开方运算.小明提出一个问题: “如果已知底数 和幕 ,求指数 是否也对应着一种运算呢?”老师首先肯定了小明善于思考,继而告诉大家这是同学们进入高中将继续学习的对数,感兴趣的同学可以课下自主探究.小明课后借助网络查到了对数的定义:

小明根据对数的定义,尝试进行了下列探究:
∵ ,∴ ;
∵ ,∴ ;
∵ ,∴ ;
∵ ,∴ ;
计算: .
三、解答题
-
18. 如图, , 交于点 , . 请你添加一个条件 , 使得 ,并加以证明.
 19. 计算:20. 先化简,再求值: ,其中x= -3.21. 解方程 .22. 解不等式组 ,并求出不等式组的整数解之和.23. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.
19. 计算:20. 先化简,再求值: ,其中x= -3.21. 解方程 .22. 解不等式组 ,并求出不等式组的整数解之和.23. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C.求证:∠A=∠D.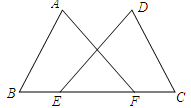 24. 下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
24. 下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,

①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵=BA,=CA,
∴点B,C分别在线段AE的垂直平分线上()(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
25. 某学校计划选购 、 两种图书.已知 种图书每本价格是 种图书每本价格的2.5倍,用1200元单独购买 种图书比用1500元单独购买 种图书要少25本.(1)、A、B两种图书每本价格分别为多少元?(2)、如果该学校计划购买 种图书的本数比购买 种图书本数的2倍多8本,且用于购买 、 两种图书的总经费不超过1164元,那么该学校最多可以购买多少本 种图书?26. 阅读:对于两个不等的非零实数 、 ,若分式 的值为零,则 或 .又因为 ,所以关于 的方程 有两个解,分别为 , .应用上面的结论解答下列问题:(1)、方程 的两个解分别为 、 ,则 , ;(2)、方程 的两个解中较大的一个为;(3)、关于 的方程 的两个解分别为 、 ( ),求 的