湖南省邵阳市双清区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-29 类型：期末考试

进入出卷网下载

一、单选题

1. 当 $x$ 为（）时，分式 $\frac{1 - x^{2}}{1 + x}$ 的值为零．

A、0 B、1 C、－1 D、2

查看试题解析
2. 下列每组数分别表示三根木棒的长度，将它们首尾连接后，能摆成三角形的一组是（）

A、1，2，5 B、2，2，4 C、1，2，3 D、2，3，4

查看试题解析
3. 2011年3月11日，里氏9.0级的日本大地震导致当天地球的自转时间较少了0.000 00016秒，将0.000 00016用科学记数法表示为（）

A、 $1.6 \times 10^{- 7}$ B、 $1.6 \times 10^{- 6}$ C、 $1.6 \times 10^{- 5}$ D、 $16 \times 10^{- 5}$

查看试题解析
4. 分式方程 $\frac{3}{2 x} = \frac{1}{x - 1}$ 的解为（）

A、x=1 B、x=2 C、x=3 D、x=4

查看试题解析
5. 下列语句是命题的是（）
⑴两点之间，线段最短；

⑵如果两个角的和是90度，那么这两个角互余.

⑶请画出两条互相平行的直线；

⑷过直线外一点作已知直线的垂线；

A、（1）（2） B、（3）（4） C、（2）（3） D、（1）（4）

查看试题解析
6. 如果把分式 $\frac{x - y}{x y}$ 中的 $x$ 和 $y$ 都扩大了3倍，那么分式的值（）

A、扩大3倍 B、不变 C、缩小3倍 D、缩小6倍

查看试题解析
7. 如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（）

A、60° B、70° C、80° D、90°

查看试题解析
8. 如图，在Rt△ACB中，∠ACB=90°，∠A=25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）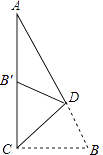

A、25° B、30° C、35° D、40°

查看试题解析
9. 式子 $\sqrt{x + 1}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x \geq 0$ B、 $x \geq - 1$ C、 $x \leq 1$ D、 $x \leq - 1$

查看试题解析
10. 下列各式中为最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{4 a}$ C、 $\sqrt{15}$ D、 $\sqrt{\frac{2}{3}}$

查看试题解析

二、填空题

11. 计算： $\frac{x}{x - 2} + \frac{2}{2 - x} =$ ．

查看试题解析
12. 若 ${(a - 3)}^{2} + | 7 - b | = 0$ ，则以 $a$ 、 $b$ 为边长的等腰三角形的周长为．

查看试题解析
13. 计算： ${(- 2019)}^{0} + | - 1 | - {(\frac{1}{2})}^{- 1} =$ ．

查看试题解析
14. 如图，点D、E分别在线段AB，AC上，AE=AD，不添加新的线段和字母，要使△ABE≌△ACD，需添加的一个条件是（只写一个条件即可）．

查看试题解析
15. 如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=12，CF=3，则AC =.

查看试题解析
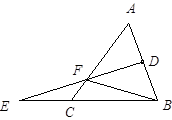16. 已知△ABC为等边三角形，BD为△ABC的高，延长BC至E ，使CE=CD=1，连接DE ，则BE= ， ∠BDE= ．

查看试题解析
17. 已知 $\frac{1}{x}$ ﹣ $\frac{1}{y}$ ＝3，则分式 $\frac{2 x + 3 x y - 2 y}{x - 2 x y - y}$ 的值为.

查看试题解析
18. 如图，已知， $∠ C A E = ∠ D A B$ ，AC=AD．给出下列条件： ①AB=AE；②BC=ED；③ $∠ C = ∠ D$ ；④ $∠ B = ∠ E$ .其中能使 $Δ A B C ≅ Δ A E D$ 的条件为（注：把你认为正确的答案序号都填上）.

查看试题解析

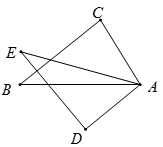
三、解答题

19. 计算： $2^{- 1} - {(- 1)}^{2019} + | \frac{1}{2} - \sqrt{2} | - {(π - 3.14)}^{0}$

查看试题解析
20. 解方程或不等式组：

(1)、 $\frac{2}{x - 3} - 2 = \frac{x - 2}{x - 3}$ ；

(2)、 ${\begin{array}{l} 5 x - 3 ⩾ 2 x \\ \frac{3 x - 1}{2} > 4 \end{array}$

查看试题解析
21. 先化简，再求值： $\frac{a - 2}{a + 3} \div \frac{a^{2} - 4}{2 a + 6} - \frac{5}{a + 2}$ ，其中 $a = - 5$ .

查看试题解析
22. 数轴上点 $A$ 表示 $\sqrt{2}$ ，点 $A$ 关于原点的对称点为 $B$ ，设点 $B$ 所表示的数为 $x$ ，

(1)、求 $x$ 的值；

(2)、求 $（ x - \sqrt{2} ）^{2} + \sqrt{2} x$ 的值.

查看试题解析
23. 如图，D是△ABC的BC边上的一点，AD=BD，∠ADC=80°.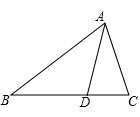

(1)、求∠B的度数；

(2)、若∠BAC=70°，判断△ABC的形状，并说明理由.

查看试题解析
24. 如图，点 $D$ 是 $A B$ 上一点， $D F$ 交 $A C$ 于点 $E$ ， $D E = F E$ ， $F C // A B$ ；求证： $A D = C F$ ．

查看试题解析

25. 为了保护环境，某开发区综合治理指挥部决定购买

A

，

B

两种型号的污水处理设备共10台．已知用90万元购买

A

型号的污水处理设备的台数与用75万元购买

B

型号的污水处理设备的台数相同，每台设备价格及月处理污水量如下表所示：

污水处理设备	$A$ 型	$B$ 型
价格（万元/台）	$m$	$m - 3$
月处理污水量（吨/台）	220	180

(1)、求m的值；

(2)、由于受资金限制，指挥部用于购买污水处理设备的资金不超过156万元，问有多少种购买方案？并求出每月最多处理污水量的吨数．

查看试题解析

26. 以点 $A$ 为顶点作等腰 $Rt Δ A B C$ ，等腰 $Rt Δ A D E$ ，其中 $∠ B A C = ∠ D A E = 90 °$ ，如图1所示放置，使得一直角边重合，连接 $B D$ 、 $C E$ ．

(1)、试判断 $B D$ 、 $C E$ 的数量关系，并说明理由；

(2)、延长 $B D$ 交 $C E$ 于点 $F$ 试求 $∠ B F C$ 的度数；

(3)、把两个等腰直角三角形按如图2放置，（1）、（2）中的结论是否仍成立？请说明理由．

查看试题解析