湖南省怀化市鹤城区2019-2020学年八年级上学期数学期末试卷

试卷更新日期：2020-12-29 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、3.14 B、 $\sqrt[3]{27}$ C、 $- \sqrt{4}$ D、 $- \sqrt{8}$

查看试题解析
2. 计算 ${(\frac{1}{2})}^{- 1}$ 的值为（）．

A、 $- \frac{1}{2}$ B、－2 C、 $\frac{1}{2}$ D、2

查看试题解析
3. 下列长度的三条线段能组成三角形的是（）

A、6cm，8cm，9cm B、4cm，4cm，10cm C、5cm，6cm，11cm D、3cm，4cm，8cm

查看试题解析
4. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{8}$ B、 $\sqrt{10}$ C、 $\sqrt{12}$ D、 $\sqrt{0.3}$

查看试题解析
5. 下列运算正确的是（）

A、 $\frac{- x}{- x + y} = \frac{x}{x - y}$ B、 $\sqrt{{(- 4)}^{2}} = - 4$ C、2^-3=-6 D、 $m^{6} \div m^{2} = m^{3}$

查看试题解析
6. 下列图形中AD是三角形ABC的高线的是（）

A、 B、 C、 D、

查看试题解析
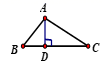7. 如图，若△ABC≌△DEF ，且BE＝5，CF＝2，则BF的长为（　　）

A、2 B、3 C、1.5 D、5

查看试题解析
8. 下列命题是假命题的是（）．

A、同旁内角互补，两直线平行 B、线段垂直平分线上的点到线段两个端点的距离相等 C、相等的角是对顶角 D、角是轴对称图形

查看试题解析
9. 不等式 $2 x + 1 > 3 + 3 x$ 的解集在数轴上表示，正确的是（）

A、 B、 C、 D、

查看试题解析
10. 若关于 $x$ 的分式方程 $\frac{m}{x - 3} = \frac{1 - x}{3 - x} - 2$ 有增根，则实数 $m$ 的值是（）

A、 $2$ B、 $- 2$ C、 $1$ D、 $0$

查看试题解析

二、填空题

11. 如果一个正数的两个平方根分别为3m+4和2﹣m，则这个数是．

查看试题解析
12. 如图，在△ABC中，∠A＝40°，点D为AB的延长线上一点，且∠CBD＝120°，则∠C＝．

查看试题解析
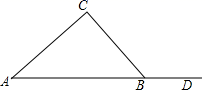13. 要测量河岸相对两点A，B的距离，已知AB垂直于河岸BF，先在BF上取两点C，D，使CD＝CB，再过点D作BF的垂线段DE，使点A，C，E在一条直线上，如图，测出DE＝20米，则AB的长是米．

查看试题解析
14. 在一次知识竞赛中，有25道抢答题，答对一题得4分，答错或不答每题扣2分，成绩不低于60分就可获奖．那么获奖至少要答对道题．

查看试题解析
15. 如果有： $\sqrt{x - 2} + | y + 1 | = 0$ ，则 $x + y$ = ．

查看试题解析
16. 若关于x的不等式组 ${\begin{array}{l} \frac{x + 3}{2} - 1 > 1 \\ \frac{x + 3}{2} - 1 < \frac{x - a}{4} \end{array}$ 有4个整数解，那么a的取值范围是．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(- 3)}^{2} - {(\sqrt{5} - 1)}^{0} + {(\frac{1}{2})}^{- 2}$

(2)、 $\sqrt{24} \div \sqrt{2} + \sqrt{27}$

查看试题解析
18. 先化简代数式 $\frac{a^{2} - 2 a + 1}{a^{2} - 4} \div (1 - \frac{3}{a + 2})$ ，再从 $2, - 2, 1, - 1,$ 四个数中选择一个你喜欢的数代入求值．

查看试题解析
19. 解方程与不等式组

(1)、解方程： $\frac{3 + x}{x - 4} + 1 = \frac{1}{4 - x}$

(2)、解不等式组 ${\begin{matrix} 3 x - 4 \leq 6 x - 2 ① \\ \frac{2 x + 1}{3} - 1 < \frac{x - 1}{2} ② \end{matrix}$

查看试题解析
20. 已知，如图A、C、F、D在同一条直线上，AF＝DC， $A B // D E$ ，AB＝DE．

求证：

(1)、 $△ A B C ≌ △ D E F$ ；

(2)、 $B C // E F$ ．

查看试题解析
21. 某商家预测“华为P30”手机能畅销，就用1600元购进一批该型号手机壳，面市后果然供不应求，又购进6000元的同种型号手机壳，第二批所购买手机壳的数量是第一批的3倍，但进货单价比第一批贵了2元．

(1)、第一批手机壳的进货单价是多少元？

(2)、若两次购进于机壳按同一价格销售，全部传完后，为使得获利不少于2000元，那么销售单价至少为多少？

查看试题解析
22. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ B A C = 120 °$ ，点 $D$ 、 $F$ 分别为 $A B$ 、 $A C$ 中点， $E D ⊥ A B$ ， $G F ⊥ A C$ ，若 $B C = 15 c m$ ，求 $E G$ 的长．

查看试题解析
23. 同学们，我们以前学过完全平方公式 $a^{2} \pm 2 a b + b^{2} = {(a \pm b)}^{2}$ ，你一定熟练掌握了吧！现在，我们又学习了二次根式，那么所有的非负数（以及0）都可以看作是一个数的平方，如 $3 = {(\sqrt{3})}^{2}$ ， $5 = {(\sqrt{5})}^{2}$ ，下面我们观察： ${(\sqrt{2} - 1)}^{2} = {(2 \sqrt{2})}^{2} - 2 \times 1 \times \sqrt{2} + 1^{2} = 2 - 2 \sqrt{2} + 1 = 3 - 2 \sqrt{2}$ ，反之， $3 - 2 \sqrt{2} = 2 - 2 \sqrt{2} + 1 = {(\sqrt{2} - 1)}^{2}$ ，∴ $3 - 2 \sqrt{2} = {(\sqrt{2} - 1)}^{2}$ ，∴ $\sqrt{3 - 2 \sqrt{2}} = \sqrt{2} - 1$
求：

(1)、 $\sqrt{3 + 2 \sqrt{2}}$ ；

(2)、 $\sqrt{4 - \sqrt{12}}$ ；

(3)、若 $\sqrt{a \pm 2 \sqrt{b}} = \sqrt{m} \pm \sqrt{n}$ ，则m、n与a、b的关系是什么？并说明理由．

查看试题解析
24.

(1)、问题发现：
如图①， $△ A B C$ 与 $△ A D E$ 是等边三角形，且点 $B$ ， $D$ ， $E$ 在同一直线上，连接 $C E$ ，求 $∠ B E C$ 的度数，并确定线段 $B D$ 与 $C E$ 的数量关系．

(2)、拓展探究：
如图②， $△ A B C$ 与 $△ A D E$ 都是等腰直角三角形， $∠ B A C = ∠ D A E = 90 °$ ，且点 $B$ ， $D$ ， $E$ 在同一直线上， $A F ⊥ B E$ 于点 $F$ ，连接 $C E$ ，求 $∠ B E C$ 的度数，并确定线段 $A F$ ， $B F$ ， $C E$ 之间的数量关系．

查看试题解析