安徽省芜湖市市区2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期：2020-12-29 类型：月考试卷
一、选择题：每小题给出的四个选项中，其中只有一个是正确的.请把正确选项的代号写在下面的答题表内（本大题共10小题，每题 4分，共40分）
-
1. 下列图形既是轴对称图形又是中心对称图形的是（ ）.A、
B、
C、
D、
2. 如果将抛物线y＝x2+2向右平移1个单位，那么所得新抛物线的顶点坐标是（ ）.A、（﹣1，﹣2） B、（﹣1，2） C、（1，2） D、（1，﹣2）3. 下列命题是真命题的是（ ）A、顶点在圆上的角叫圆周角 B、三点确定一个圆 C、圆的切线垂直于半径 D、三角形的内心到三角形三边的距离相等4. 如图所示，AB为⊙O的直径，点C在⊙O上．若∠C=16°，则∠BOC的度数是（ ）.
A、74 B、48° C、32° D、16°5. 一个排水管的截面如图所示，已知截面圆半径OB=10，圆心O到水面的距离OC是6，则水面宽AB是（ ）.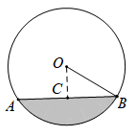
A、16 B、10 C、8 D、66. 如图所示，AB是⊙O 的弦，点C 在过点B的切线上，OC⊥OA ，OC 交AB 于点P .若∠BPC=70°，则∠ABC的度数等于（ ）.
A、75° B、70° C、65° D、60°7. 已知圆锥的母线长为6，将其侧面沿着一条母线展开，所得扇形的圆心角为120°，则该扇形面积是（ ）.A、4π B、8π C、12π D、16π8. 某网店在“双11”促销活动中对一件原价500元的商品进行了“折上折”优惠活动(即两次打折数相同)，优惠后实际仅售320元，设该店打x折，则可列方程（ ）.A、 B、 C、 D、9. 二次函数y=－x2+2x+4，当－1≤x≤2时，则（ ）.A、1≤y≤4 B、y≤5 C、4≤y≤5 D、1≤y≤510. 把抛物线y＝ax2+bx+c（a＞0）作关于x轴的对称变换，所得图象的解析式为y＝－a（x－1）2+4a ， 若(m－1)a+b+c≤0，则m的最大值是（ ）.A、6 B、2 C、0 D、－4二、填空题 （本大题共4小题，每小题5分，满分20分）
-
11. 若 是关于x的一元二次方程，则m的值为 ．12. 如图所示，A、B、C、D 是一个正n边形的顶点，O为其中心，若∠ADB=18°，则n=
13. 如图所示，⊙O是△ABC的外接圆，∠ABC=30°，AC=6，则的长为.
14. 如图所示，点P为⊙O外一点，过点P作⊙O的切线PA、PB ， 点A、B为切点．连接AO并延长交PB 的延长线于点C ， 过点C作CD⊥PO ， 交PO的延长线于点D ．
(1)、=(2)、若PA=6，AC=8，则CD=三、（本大题共2小题，每小题8分，满分16分）
-
15. 解方程x(x－2)=5(x－2).16. 如图，在平面直角坐标系中，△ABC的顶点坐标为A(－3，4)，B(－4，2)，C(－2，1)，将△ABC绕原点O顺时针旋转90°，得到△A1B1C1 ， ΔA1B1C1向左平移2个单位，再向下平移5个单位得到△A2B2C2.
(1)、分别画出△A1B1Cl和△A2B2C2；(2)、设P(a ， b)是△ABC的AC边上一点，△ABC经旋转、平移后点P的对应点分别为P1 ， P2 ， 请直接写出点P1和P2的坐标.四、（本大题共2小题，每小题8分，满分16分）
-
17. 已知关于x的一元二次方程x2－2x－k＝0有两个不相等的实数根.(1)、求k的取值范围；(2)、若 是该方程的一个实根，求k的值.18. 如图所示，在 Rt△ABC中，∠C=90°，AC=4 ，BC=3 .求以直角边所在直线为轴，把△ABC 旋转一周得到的圆锥的侧面积.
五、（本大题共2小题，每小题10分，满分20分）
-
19. 如图，在△ABC中，AC=BC ， D是AB上一点，⊙O经过点A ， C ， D ， 过点D作DE∥BC ， 交⊙O于点E ， 连接CE.
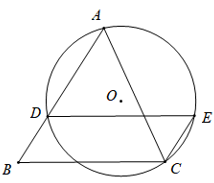
求证：四边形DBCE是平行四边形.
20. 已知：对称轴为x＝1的抛物线经过A（－1，0），B（2，－3）两点．(1)、求该抛物线的解析式；(2)、设点P是该抛物线在第四象限内的图象上的一个动点，连接PO交直线AB于点Q ，当Q是OP中点时，试求点P的坐标.
六、（本题满分12分）
-
21. 如图，AB是⊙O的直径，AE是弦，C是劣弧AE的中点，过C作CD⊥AB于点D ， CD交AE于点F ， 过C作CG∥AE交BA的延长线于点G.
(1)、求证：CG是⊙O的切线；(2)、求证：AF=CF；(3)、若∠EAB=30°，CF=2，求GA的长.七、（本题满分12分）
-
22. 某服装厂生产A品种服装，每件成本为71元，零售商到此服装厂一次性批发A品牌服装x件时，批发单价为y元，y与x之间满足如下图所示的函数关系，其中批发件数x为10的正整数倍.
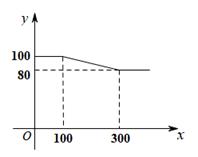(1)、当100≤x≤300 时，则y与x的函数关系式为；(2)、某零售商到此服装厂一次性批发A品牌服装200件，需要支付元；(3)、若零售商到此服装厂一次性批发A品牌服装x(100≤x≤400) 件，服装厂的利润为w元，求：x 为何值时，w最大？最大值是多少？八、（本题满分14分）
-
23. 在△ADC和△BEC中，AD=CD ， BE=CE ， ∠ADC=∠BEC=90°，且BC＜CD ， 将△BEC绕点C逆时针旋转，连接AB ， 设点O为线段AB的中点，连接DO和EO.
(1)、如图1，当点B在CD边上时，求证：DO=EO ， DO⊥EO；(2)、如图2，在△BEC绕点C逆时针旋转的过程中，当点B 旋转至BC在AC左侧且∠ACB=60°的位置时，（1）中的结论是否成立？若成立，请写出证明过程，若不成立，请说明理由.(3)、在（2）的条件下，若BC=4，CD= ，求OD的长.
-
-