初中数学浙教版2020-2021年七年级上学期数学期末测试模拟卷

试卷更新日期：2020-12-28 类型：期末考试

进入出卷网下载

一、单选题

1. 如果温度上升 $10^{\circ} C$ 记作 $+ 10^{\circ} C$ ，那么温度下降 $5^{\circ} C$ 记作（）

A、 $+ 10^{\circ} C$ B、 $- 10^{\circ} C$ C、 $+ 5^{\circ} C$ D、 $- 5^{\circ} C$

查看试题解析
2. 山东省计划到2022年建成54700000亩高标准农田，其中54700000用科学记数法表示（）

A、5.47×10⁸ B、0.547×10⁸ C、547×10⁵ D、5.47×10⁷

查看试题解析
3. 下列计算：① ${(- \frac{1}{2})}^{2} = \frac{1}{4}$ ；② ${(\frac{2}{5})}^{2} = \frac{4}{5}$ ；③ ${(- 0.2)}^{3} = 0.008$ ；④ $- 3^{2} = 9$ ；⑤ $- {(- \frac{1}{3})}^{2} = \frac{1}{9}$ ．其中正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列去括号正确的是（）

A、 $x^{2} - 3 (x - y + z) = x^{2} - 3 x + 3 y + 3 z$ B、 $3 x - [5 x - (2 x - 1)] = 3 x - 5 x - 2 x + 1$ C、 $a + (- 3 x + 2 y - 1) = a - 3 x + 2 y - 1$ D、 $- (2 x - y) + (2 - 1) = - 2 x - y + 2 - 1$

查看试题解析
5. 与-a²bc³是同类项的是（）

A、2a²b³c B、5c³b²a C、-2ab³c² D、-3c³a²b

查看试题解析
6. 下列说法错误的是（）

A、 $2 π r^{2}$ 的次数是3 B、2是单项式 C、 $x y + 1$ 是二次二项式 D、多项式 $- 4 a^{2} b + 3 a b - 5$ 的常数项为-5

查看试题解析
7. 下列方程的变形，正确的是（）

A、由3+x＝5，得x＝5+3 B、由7x＝﹣4，得x＝ $- \frac{7}{4}$ C、由 $\frac{1}{2}$ y＝0，得y＝2 D、由x+3＝﹣2，得x＝﹣2﹣3

查看试题解析
8. 由四舍五入法得到的近似数6.18万，下列说法正确的是（）

A、精确到万位 B、精确到百位 C、精确到千分位 D、精确到百分位

查看试题解析
9. 某服装店新开张，第一天销售服装a件，第二天比第一天少销售14件，第三天的销售量是第二天的2倍还多10件，则这三天销售了（）件

A、3a-42 B、3a＋42 C、4a-32 D、4a＋32

查看试题解析
10. 下列说法：
①2018个有理数相乘，其中负数有2005个，那么所得的积为负数②若m满足|m|＋m＝0则m<0③有理数 $\frac{b}{a}$ 的倒数是 $\frac{a}{b}$ ④若三个有理数a，b，c满足 $\frac{| a b |}{a b} + \frac{| a c |}{a c} + \frac{| b c |}{b c}$ =-1，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = - 1$ 其中正确的是有（）个

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

11. 64的立方根是， 16的平方根是．

查看试题解析
12. 若关于x的两个多项式2x³﹣8x²+x﹣1与3x³+2mx²﹣5x+3的和为三次三项式，则m的值为.

查看试题解析
13. 已知 $(m - 3) x^{3} y^{| m | + 1}$ 是关于x ， y的七次单项式，则 $m^{2} - 2 m + 2$ 的值为

查看试题解析
14. 已知 $x^{2} + 3 x - 1 = 0$ ，则 $2 x^{2} + 6 x + 2018 =$ ．

查看试题解析
15. 已知：|a+2|+(b+1)²取最小值，则ab+ $\frac{a}{b}$ =。

查看试题解析
16. 如图所示的日历中，任意圈出-竖列相邻的三个数，设中间的一个数为a，则这三个数之和为。(用含a的代数式表示)

查看试题解析

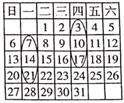
三、解答题

17. 有8个数，请分类：将序号填在相应横线上
①＋5    ② - $\frac{1}{2}$    ③－27    ④0    ⑤ $\frac{22}{7}$    ⑥10%    ⑦2.3    ⑧ $| - \frac{2}{3} |$

整数：{                …}；

正分数：{               …}；

非负数：{               …}．

查看试题解析
18. 计算

(1)、﹣24×（﹣ $\frac{5}{6} + \frac{3}{8} - \frac{1}{12}$ ）

(2)、﹣1²⁰¹⁸÷（ $\frac{1}{3} - \frac{1}{2}$ ）²﹣|﹣2|

查看试题解析
19. 如图，已知点A，B，C，D，请按要求画出图形.

①画直线AB和射线CB；

②连结AC，并在直线AB上用尺规作线段AE，使 $A E = 2 A C$ .（要求保留作图痕迹）

③在直线AB上确定一点P，使 $P C + P D$ 的和最短，并写出画图的依据.

查看试题解析
20. 在学习《实数》内容时，我们通过“逐步逼近”的方法可以计算出 $\sqrt{2}$ 的近似值，得出1.4＜ $\sqrt{2}$ ＜1.5.利用“逐步逼近“法，请回答下列问题：

(1)、 $\sqrt{19}$ 介于连续的两个整数a和b之间，且a＜b，那么a= ， b=.

(2)、x是 $\sqrt{19}$ +2的小数部分，y是 $\sqrt{19}$ −1的整数部分，则x= ， y=.

(3)、在（2）的条件下，求（ $\sqrt{19}$ −x）^y的平方根.

查看试题解析
21. 已知数轴上有A、B、C三点，分别表示有理数－26，－10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒.

(1)、用含t的代数式表示P到点A和点C的距离：PA= ， PC=。

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，当点P运动到点C时，P、Q两点运动停止，
①当P、Q两点运动停止时，求点P和点Q的距离；

②求当t为何值时P、Q两点恰好在途中相遇.

查看试题解析
22. 直线AB与直线CD相交于点O，OE平分 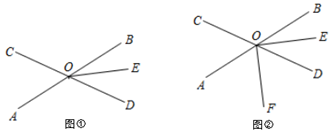$∠ B O D$ .

(1)、如图①，若 $∠ B O C = 130^{°}$ ，求 $∠ A O E$ 的度数；

(2)、如图②，射线OF在 $∠ A O D$ 内部.
①若 $O F ⊥ O E$ ，判断OF是否为 $∠ A O D$ 的平分线，并说明理由；

②若OF平分 $∠ A O E$ ， $∠ A O F = \frac{5}{3} ∠ D O F$ ，求 $∠ B O D$ 的度数.

查看试题解析

23. 某垃圾处理厂，对不可回收垃圾的处理费用为90元/吨，可回收垃圾的分拣处理费用也为90元/吨，分拣后再被相关企业回收，回收价格如下表：

垃圾种类	纸类	塑料类	金属类	玻璃类
回收单价(元/吨)	500	800	500	200

据了解，可回收垃圾占垃圾总量的60%，现有A，B，C三个小区12月份产生的垃圾总量分别为100吨，100吨和m吨。

(1)、已知A小区金属类垃圾质量是塑料类的5倍，纸类垃圾质量是塑料类的2倍。设塑料类的质量为x吨，则A小区可回收垃圾有吨，其中玻璃类垃圾有吨(用含x的代数式表示)

(2)、B小区纸类与金属类垃圾总量为35吨，当月可回收垃圾回收总金额扣除所有垃圾处理费后，收益16500元，求12月份该小区可回收垃圾中塑料类垃圾的质量。

(3)、C小区发现塑料类与玻璃类垃圾的回收总额恰好相等，所有可回收垃圾的回收总金额为12000元，设该小区塑料类垃圾质量为a吨，求a与m的数量关系。

查看试题解析

24. “十一”期间，小聪跟爸爸一起去A市旅游，出发前小聪从网上了解到A市出租车收费标准如下：
行程（千米）
3千米以内
满3千米但不超过8千米的部分
8千米以上的部分
收费标准（元）
10元
2.4元/千米
3元/千米

(1)、若甲、乙两地相距8千米，乘出租车从甲地到乙地需要付款多少元？

(2)、小聪和爸爸从火车站乘出租车到旅馆，下车时计费表显示17.2元，请你帮小聪算一算从火车站到旅馆的距离有多远？

(3)、小聪的妈妈乘飞机来到A市，小聪和爸爸从旅馆乘出租车到机场去接妈妈，到达机场时计费表显示70元，接完妈妈，立即沿原路返回旅馆（接人时间忽略不计），请帮小聪算一下乘原车返回和换乘另外的出租车，哪种更便宜？

查看试题解析

行程（千米）	3千米以内	满3千米但不超过8千米的部分	8千米以上的部分
收费标准（元）	10元	2.4元/千米	3元/千米