初中数学苏科版七年级上学期期末复习专题15 垂直

试卷更新日期：2020-12-28 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，测量运动员跳远成绩选取的是AB的长度，其依据是（）

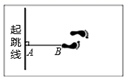A、两点确定一条直线 B、垂线段最短 C、两点之间线段最短 D、两点之间直线最短

查看试题解析
2. 已知直线AB，CB，l在同一平面内，若AB⊥l，垂足为B，CB⊥l，垂足也为B，则正确图形可以是（）

A、 B、 C、 D、

查看试题解析
3. 已知：OA⊥OC，∠AOB∶∠AOC＝2∶3，则∠BOC的度数为（）.

A、30° B、60° C、150° D、30°或150°

查看试题解析
4. 如图，AC⊥BF，CD⊥AB于点D，点E在线段BF上，则下列说法错误的是（）

A、线段CD的长度是点C到直线AB的距离 B、线段CF的长度是点C到直线BF的距离 C、线段EF的长度是点E到直线AC的距离 D、线段BE的长度是点B到直线CD的距离

查看试题解析
5. 下列说法：①在同一平面内，过一点能作已知直线的一条垂线；②在同一平面内，过一点有且只有一条直线与已知直线平行；③直线外一点与直线上各点连接的所有线段中，垂线段最短；④两条直线被第三条直线所截，内错角相等.其中正确说法的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 下列说法正确的有（）
①两条直线相交，交点叫垂足；

②在同一平面内，过一点有且只有一条直线与已知直线垂直；

③在同一平面内，一条直线有且只有一条垂线；

④在同一平面内，一条线段有无数条垂线；

⑤过一点可以向一条射线或线段所在的直线作垂线；

⑥若 $l_{1} ⊥ l_{2}$ ，则 $l_{1}$ 是 $l_{2}$ 的垂线， $l_{2}$ 不是 $l_{1}$ 的垂线.

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 如图， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，垂足为 $D$ ，则下面的结论中，正确的有（）
① $B C$ 与 $A C$ 互相垂直；②点 $A$ 到 $B C$ 的垂线段是线段 $B C$ ；③ $A C$ 与 $C D$ 互相垂直；④点 $C$ 到 $A B$ 的垂线段是线段 $C D$ ；⑤线段 $B C$ 是点 $B$ 到 $A C$ 的距离；⑥线段 $A C$ 的长度是点 $A$ 到 $B C$ 的距离

A、5个 B、4个 C、3个 D、2个

查看试题解析
8. 若线段AP，AQ分别是△ABC边上的高线和中线，则（）

A、AP＞AQ B、AP≥AQ C、AP＜AQ D、AP≤AQ

查看试题解析
9. 若点 $P$ 为直线 $l$ 外一定点，点 $A$ 为直线 $l$ 上一定点，且 $P A = 2$ ，点 $P$ 到直线 $l$ 的距离为 $d$ ，则 $d$ 的取值范围为（）

A、 $0 < d < 2$ B、 $d = 2$ 或 $d > 2$ C、 $0 < d < 2$ 或 $d = 0$ D、 $0 < d < 2$ 或 $d = 2$

查看试题解析
10. 如图所示，∠BAC=90°，AD⊥BC，则下列结论中，正确的个数为（   ）

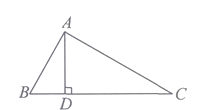
    ①AB⊥AC； ②AD与AC互相垂直； ③点C到AB的垂线段是线段AB；
    ④点A到BC的距离是线段AD的长度； ⑤线段AB的长度是点B到AC的距离；
    ⑥AD+BD>AB．

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

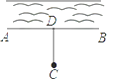
11. 如图，计划在河边建一水厂，可过C点作CD⊥AB于D点．在D点建水厂，可使水厂到村庄C的路程最短，这样设计的依据是．

查看试题解析
12. 如图， $∠ 1 = 28^{°} ， A B ⊥ C D ，$ 垂足为O， $E F$ 经过点O．则 $∠ 2$ 的度数是．

查看试题解析
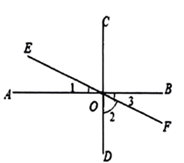13. 如图，线段AB=15cm ，线段AD=12cm ，线段AC=9cm ，则点A到BC的距离为 cm ．

查看试题解析
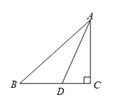14. 已知直线 $a / / b$ ，a与b之间的距离为5，a与b之间有一点P，点P到a的距离是2，则点P到b的距离是．

查看试题解析
15. 如图，直线AB，CD，EF交于点O，且AB⊥CD，∠1=22°，则∠2= ， ∠FOB= ．

查看试题解析
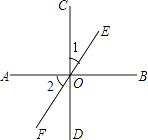16. 如图，点O为直线AB上一点，∠1=20°，当∠2=时，OC⊥OD．

查看试题解析
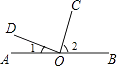17. 已知 $∠ A$ 的两边与∠B的两边分别垂直，且 $∠ A$ 比∠B的3倍少 $40^{°}$ ，那么 $∠ A =$ $^{°}$

查看试题解析
18. 如图，将一副直角三角板放在同一条直线AB上，其中∠ONM=30°，∠OCD=45°．将三角尺OCD绕点O按每秒30°的速度沿顺时针方向旋转一周，在旋转的过程中，当第秒时，直线CD恰好与直线MN垂直．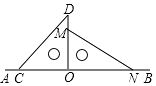

查看试题解析

三、综合题

19. 直线AB、CD相交于点O.OE、OF分别是∠AOC、∠BOD的平分线.

(1)、画出这个图形.

(2)、射线OE、OF在同一条直线上吗?

(3)、画∠AOD的平分线OG.OE与OG有什么位置关系?并说明理由.

查看试题解析
20. 如图，直线AB、CD相交于点O，EO⊥AB，垂足为O，∠EOC：∠AOD=7：11，求∠DOE的度数.

查看试题解析
21. 如图，直线AB、CD相交于点O，OM⊥AB.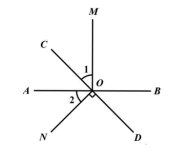

(1)、若∠1=∠2，证明：ON⊥CD；

(2)、若 $∠ 1 = \frac{1}{3} ∠ B O C$ ，求∠BOD的度数.

查看试题解析
22. 已知：如图，直线AB、CD相交于点O，EO⊥CD于O．

(1)、若∠AOC=36°，求∠BOE的度数；

(2)、若∠BOD：∠BOC=1：5，求∠AOE的度数；

(3)、在（2）的条件下，请你过点O画直线MN⊥AB，并在直线MN上取一点F（点F与O不重合），然后直接写出∠EOF的度数．

查看试题解析
23. 如图，直线AB，CD相交于点O，∠AOC=60°，∠1∶∠2=1：2．

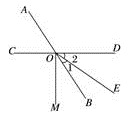(1)、求∠2的度数；

(2)、若∠2与∠MOE互余，求∠MOB的度数．

查看试题解析
24. 已知：直线AB，CD相交于点O，且OE⊥CD，如图.

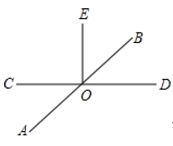(1)、过点O作直线MN⊥AB；

(2)、若点F是（1）中所画直线MN上任意一点（O点除外），且∠AOC=35°，求∠EOF的度数；

(3)、若∠BOD：∠DOA=1：5，求∠AOE的度数.

查看试题解析
25. 如图， $A B$ 交 $C D$ 于 $O$ ， $O E ⊥ A B$ ．

(1)、若 $∠ E O D = 30 °$ ，求 $∠ A O C$ 的度数；

(2)、若 $∠ E O D ： ∠ E O C = 1 ： 3$ ，求 $∠ B O C$ 的度数．

查看试题解析
26. 如图，已知∠AOB， OE平分∠AOC， OF平分∠BOC.

(1)、若∠AOB是直角，∠BOC＝60°，求∠EOF的度数；

(2)、猜想∠EOF与∠AOB的数量关系；

(3)、若∠AOB＋∠EOF＝156°，则∠EOF是多少度？

查看试题解析