初中数学苏科版七年级上学期期末复习专题13 角
试卷更新日期:2020-12-28 类型:复习试卷
一、单选题
-
1. 甲以 点出发治北偏西30°走了50米到达 点,乙从 点出发,沿南偏东60°方向走了80米到达 点,那么 为( )A、150° B、120° C、180° D、190°2. 下列说法中正确的是( )A、如果 ,那么x一定是7 B、 表示的数一定是负数 C、射线AB和射线BA是同一条射线 D、一个锐角的补角比这个角的余角大90°3. 下列关于余角、补角的说法,正确的是( )A、若∠1+∠2+∠3=90°,则∠1、∠2、∠3互余 B、若∠α+∠β+∠γ=180°,则∠α、∠β、∠γ互补 C、若∠1+∠2=90°,则∠1与∠2互补 D、若∠α+∠β=90°,则∠α与∠β互余4. 将一副三角尺按如图方式摆放,若 ,则 的度数等于( ).
 A、 B、 C、 D、5. 如图所示, , ,则图中互为余角的共有( )
A、 B、 C、 D、5. 如图所示, , ,则图中互为余角的共有( )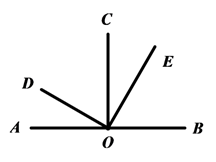 A、5对 B、4对 C、3对 D、2对6. 已知∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的 ,∠则∠1,∠2,∠3的度数分别为( )A、50°,40°,130° B、60°,30°,120° C、70°,20°,110° D、75°,15°,105°7. 已知点O是直线AB上一点, ,OD平分 , ,下列结果,错误的是( )
A、5对 B、4对 C、3对 D、2对6. 已知∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的 ,∠则∠1,∠2,∠3的度数分别为( )A、50°,40°,130° B、60°,30°,120° C、70°,20°,110° D、75°,15°,105°7. 已知点O是直线AB上一点, ,OD平分 , ,下列结果,错误的是( ) A、∠BOC=130° B、∠AOD=25° C、∠BOD=155° D、∠COE=45°8. 下列说法中:①-a一定是一个负数;②经过两点有一条直线,并且只有一条直线;③一个锐角的补角一定大于它的余角;④绝对值最小的有理数是1;⑤倒数等于它本身的数只有1,正确的个数有( )A、1个 B、2个 C、3个 D、4个9. 如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中:①90°﹣∠α;②∠β﹣90°;③ (∠α+∠β);④ (∠β﹣∠α)其中正确的有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )
A、∠BOC=130° B、∠AOD=25° C、∠BOD=155° D、∠COE=45°8. 下列说法中:①-a一定是一个负数;②经过两点有一条直线,并且只有一条直线;③一个锐角的补角一定大于它的余角;④绝对值最小的有理数是1;⑤倒数等于它本身的数只有1,正确的个数有( )A、1个 B、2个 C、3个 D、4个9. 如果∠α和∠β互补,且∠α<∠β,则下列表示∠α的余角的式子中:①90°﹣∠α;②∠β﹣90°;③ (∠α+∠β);④ (∠β﹣∠α)其中正确的有( )A、1个 B、2个 C、3个 D、4个10. 如图,已知A,O,B在一条直线上,∠1是锐角,则∠1的余角是( )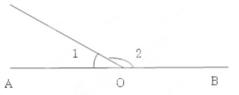 A、 B、 C、 D、∠2-∠1
A、 B、 C、 D、∠2-∠1二、填空题
-
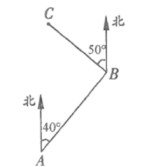
11. 若∠1+∠2=180°,∠1+∠3=180°,则∠2与∠3的关系是.12. 已知一个角的补角是它余角的3倍,则这个角的度数为.13. 如图,点B在点A北偏东40°方向,点C在点B北偏西50° 方向, BC=10m,则点 C到直线 AB的距离为 m.
 14. 计算: .15. 如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE= .
14. 计算: .15. 如图,已知直线AD、BE、CF相交于O,OG⊥AD,且∠BOC=35°,∠FOG=30°,则∠DOE= .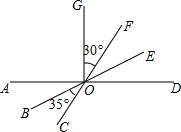 16. 如图,将一副三角板的直角顶点重合在一起,其中 和 是直角,若 ,则 的度数是.
16. 如图,将一副三角板的直角顶点重合在一起,其中 和 是直角,若 ,则 的度数是. 17. 已知在同一平面内,
17. 已知在同一平面内,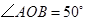 ,
,  ,则
,则  . 18. 在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是.
. 18. 在∠AOB中,C,D分别为边OA,OB上的点(不与顶点O重合).对于任意锐角∠AOB,下面三个结论中,①作边OB的平行线与边OA相交,这样的平行线能作出无数条;②连接CD,存在∠ODC是直角;③点C到边OB的距离不超过线段CD的长.所有正确结论的序号是.三、解答题
-
19. 如图,直线AB、CD相交于点O,OE平分∠BOD,∠AOC=72°,OF⊥CD,垂足为O,求∠EOF和∠AOE的度数。
 20. 如图,已知 、 、 三点在一条直线上, 平分 , ,判断 和 之间有怎样的关系,并说明理由.
20. 如图,已知 、 、 三点在一条直线上, 平分 , ,判断 和 之间有怎样的关系,并说明理由. 21. 如图,货轮 在航行过程中,发现灯塔 在它北偏东 的方向上,同时,在它南偏西 、西北(即北偏西 )方向上又分别发现了客轮 和海岛 ,仿照表示灯塔方位的方法,画出表示客轮 和海岛 方向的射线.
21. 如图,货轮 在航行过程中,发现灯塔 在它北偏东 的方向上,同时,在它南偏西 、西北(即北偏西 )方向上又分别发现了客轮 和海岛 ,仿照表示灯塔方位的方法,画出表示客轮 和海岛 方向的射线. 22. 已知如图,直线 相交于点 .
22. 已知如图,直线 相交于点 .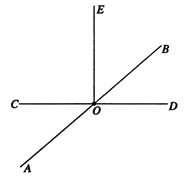 (1)、若∠AOC=35°,求 的度数;(2)、若∠BOD:∠BOC=2:4,求 的度数;(3)、在(2)的条件下,过点 作 ,求 的度数.23. 如图所示,已知∠BAC=∠EAD=90o.
(1)、若∠AOC=35°,求 的度数;(2)、若∠BOD:∠BOC=2:4,求 的度数;(3)、在(2)的条件下,过点 作 ,求 的度数.23. 如图所示,已知∠BAC=∠EAD=90o.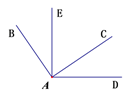 (1)、判断∠BAE与∠CAD的大小关系,并说明理由.(2)、当∠EAC=60o时,求∠BAD的大小.(3)、探究∠EAC与∠BAD的数量关系,请直接写出结果,不要求说明理由.24. 将一副三角板放在同一平面内,使直角顶点重合于点O
(1)、判断∠BAE与∠CAD的大小关系,并说明理由.(2)、当∠EAC=60o时,求∠BAD的大小.(3)、探究∠EAC与∠BAD的数量关系,请直接写出结果,不要求说明理由.24. 将一副三角板放在同一平面内,使直角顶点重合于点O
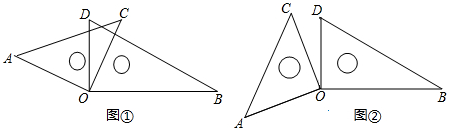 (1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.25. 如图1,点O为直线AB上一点,过点O作射线OC , 使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)、如图①,若∠AOB=155°,求∠AOD、∠BOC、∠DOC的度数.(2)、如图①,你发现∠AOD与∠BOC的大小有何关系?∠AOB与∠DOC有何关系?直接写出你发现的结论.(3)、如图②,当△AOC与△BOD没有重合部分时,(2)中你发现的结论是否还仍然成立,请说明理由.25. 如图1,点O为直线AB上一点,过点O作射线OC , 使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方. (1)、在图1中,∠AOC=°,∠MOC=°;(2)、将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;(3)、将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.26. 定义:若 ,且 ,则我们称 是 的差余角.例如:若 ,则 的差余角 .
(1)、在图1中,∠AOC=°,∠MOC=°;(2)、将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;(3)、将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.26. 定义:若 ,且 ,则我们称 是 的差余角.例如:若 ,则 的差余角 .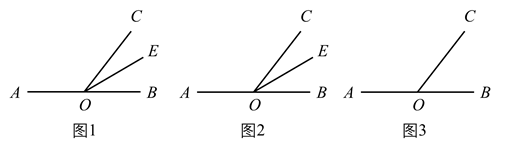 (1)、如图1,点O在直线 上,射线 是 的角平分线,若 是 的差余角,求 的度数.(2)、如图2,点O在直线 上,若 是 的差余角,那么 与 有什么数量关系.(3)、如图3,点O在直线 上,若 是 的差余角,且 与 在直线 的同侧,请你探究 是否为定值?若是,请求出定值;若不是,请说明理由.
(1)、如图1,点O在直线 上,射线 是 的角平分线,若 是 的差余角,求 的度数.(2)、如图2,点O在直线 上,若 是 的差余角,那么 与 有什么数量关系.(3)、如图3,点O在直线 上,若 是 的差余角,且 与 在直线 的同侧,请你探究 是否为定值?若是,请求出定值;若不是,请说明理由.