初中数学苏科版七年级上学期期末复习专题12 线段、射线和直线

试卷更新日期：2020-12-28 类型：复习试卷

进入出卷网下载

一、单选题

1. 在下列生活、生产现象中，可以用基本事实“两点确定一条直线”来解释的是（）
①用两颗钉子就可以把木条固定在墙上；②把笔尖看成一个点，当这个点运动时便得到一条线；③把弯曲的公路改直，就能缩短路程；④植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上.

A、 $① ③$ B、 $② ④$ C、 $① ④$ D、 $② ③$

查看试题解析
2. 如图，某同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长小，能正确解释这一现象的数学知识是：（）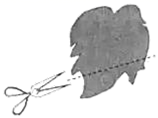

A、两点之间，直段最短 B、两点确定一条直线 C、两点之间，线段最短 D、经过一点有无数条直线

查看试题解析
3. 如图，下列错误的说法是（）

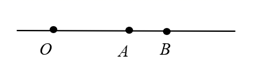A、直线 $A B$ 与直线 $B A$ 是同一条直线 B、射线 $O A$ 与射线 $A B$ 是同一条射线 C、线段 $A B$ 与线段 $B A$ 是同一条线段 D、射线 $O A$ 与射线 $O B$ 是同一条射线

查看试题解析
4. 数轴上表示数a和数b的两点之间的距离为5，若a的相反数为2，则b为（）

A、－7 B、－3 C、3 D、3或－7

查看试题解析
5. $M$ 点在数轴上表示 $- 4$ ， $N$ 点离 $M$ 的距离是 $3$ ，那么 $N$ 点表示（）

A、-1 B、-7 C、-1或-7 D、-1或1

查看试题解析
6. 如果线段AB=3cm，BC=1cm，那么A、C两点的距离d的长度为（　　）

A、4cm B、2cm C、4cm或2cm D、小于或等于4cm，且大于或等于2cm

查看试题解析
7. 如图，数轴上标出若干个点，每相邻两个点的距离为1个单位，点E、F、M、N对应的数分别为a、b、c、d，且d－2a＝8，那么数轴的原点是（）

A、E点 B、F点 C、M点 D、N点

查看试题解析
8. 当式子|x+1|+|x﹣6|取得最小值时，x的取值范围为（）

A、﹣1≤x＜6 B、﹣1≤x≤6 C、x=﹣1或x=6 D、﹣1＜x≤6

查看试题解析
9. 有三个点A，B，C，过其中每两个点画直线，可以画出直线（　　）

A、1条 B、2条 C、1条或3条 D、无法确定

查看试题解析
10. 平面内的9条直线任两条都相交，交点数最多有m个，最少有n个，则m+n等于（　　）

A、36 B、37 C、38 D、39

查看试题解析

二、填空题

11. 数轴上与表示数1的点的距离为8个单位长度的点所表示的数是．

查看试题解析
12. 一条直线上有A、B、C、D四个点，则图中共有条线段．

查看试题解析
13. 数轴上点A所表示的数是－18,点B到点A的距离是17,则点B所表示的数是．

查看试题解析
14. 如图，数轴的单位长度为1，当点B为原点时，若存在一点M到A的距离是点M到D 的距离的2倍，则点M所表示的数是．

查看试题解析
15. 点A、B、C在同一条直线上，其中点A、B表示的数分别为-3、1，若C点到B点的距离为2，则A点与C点之间的距离是.

查看试题解析
16.
如图，已知C、D是AB上两点，且AB=20cm，CD=6cm，M是AD的中点，N是BC的中点，则线段MN的长为cm．

查看试题解析
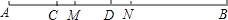17. 点 $A, B, C$ 在同一条数轴上，且点 $A$ 表示的数为－1，点 $B$ 表示的数为5.若 $B C = 2 A C$ ，则点 $C$ 表示的数为.

查看试题解析
18. 已知A，B，C是数轴上的三个点，点A，B表示的数分别是1，3.如图所示，若BC=2AB，则点C表示的数是．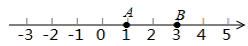

查看试题解析

三、解答题

19. 如图，平面上四个点A，B，C，D．按要求完成下列问题：

(1)、连接AD，BC；

(2)、画射线AB与直线CD；

(3)、在图中找到一点H，使它与四点的距离最小．

查看试题解析
20.
如图所示，线段AB=6cm，点C是线段AB上任意一点，点M是线段AC的中点，点N是线段BC的中点，求线段MN的长．

查看试题解析
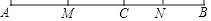21. 如图，已知AB：BC：CD=2：3：4，E、F分别为AB、CD中点，且EF=15．求线段AD的长．

查看试题解析
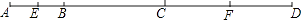22.

(1)、如图，点C是线段AB上一点，点M、N分别是AC、BC的中点．

①若AC＝8cm，CB＝6cm，请求出线段MN的长；

②若点C满足AC+CB＝acm，其它条件不变，你能猜想MN的长度吗？请说明理由；

(2)、若C在线段AB的延长线上，且满足AC﹣BC＝bcm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由．

查看试题解析
23. 阅读下面材料：
若点A、B在数轴上分别表示数a，b，则A、B两点之间的距离表示为|AB|

(1)、数轴上表示2和5两点之间的距离是，数轴上表示-3和4两点之间的距离是．

(2)、若数轴上点B表示的数是-1，且|AB| = 3，则a= ．

(3)、在数轴上有三个点A， B， C若点A表示的数是-1，点B表示的数是3，且|AB| + |AC| = 6 ，求点C表示的数．

查看试题解析
24.

(1)、数轴上表示4和1的两点之间的距离是；表示﹣3和2两点之间的距离是；一般地，数轴上表示数m和数n的两点之间的距离等于|m﹣n|．如果表示数a和﹣2的两点之间的距离是3，那么a＝．

(2)、已知A、B、C为数轴上三点，当点C到点A的距离是点C到点B的距离3倍时，则称点C是（A ， B）的三倍点，不是（B ， A）的三倍点．若A、B点表示的数分别为﹣1，3．
①若点C是（A ， B）的三倍点，求点C表示的数；

②若点C在点A的左边，是否存在使得A、B、C中恰有一个点为其余两点的三倍点．

查看试题解析
25. 如图，已知数轴上有A、B、C三个点，它们表示的数分别是18，8，﹣10．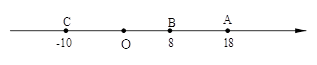

(1)、填空：AB= ， BC=；

(2)、若点A以每秒1个单位长度的速度向右运动，同时，点B和点C分别以每秒2个单位长度和5个单位长度的速度向左运动．试探索：BC﹣AB的值是否随着时间t的变化而改变？请说明理由．

(3)、现有动点P、Q都从A点出发，点P以每秒1个单位长度的速度向终点C移动；当点P移动到B点时，点Q才从A点出发，并以每秒3个单位长度的速度向左移动，且当点P到达C点时，点Q就停止移动．设点P移动的时间为t秒，试用含t的代数式表示P、Q两点间的距离．

查看试题解析
26. 在学习绝对值后，我们知道， $| a |$ 表示数a在数轴上的对应点与原点的距离，如：5表示5在数轴上的对应点到原点的距离.而 $| 5 | = | 5 - 0 |$ ，即 $| 5 - 0 |$ 表示5、0在数轴上对应的两点之间的距离，类似的，有： $| 5 - 3 |$ 表示5、3在数轴上对应的两点之间的距离； $| 5 + 3 | = | 5 - (- 3) |$ ，所以 $| 5 + 3 |$ 表示5、-3在数轴上对应的两点之间的距离一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为 $| a - b |$ .
请根据绝对值的意义并结合数轴解答下列问题：

(1)、数轴上表示2和3的两点之间的距离是；数轴上P、Q两点的距离为3，点P表示的数是2，则点Q表示的数是.

(2)、点A、B、C在数轴上分别表示有理数x、-3、1，那么A到B的距离与A到C的距离之和可表示为（用含绝对值的式子表示）；满足 $| x - 3 | + | x + 2 | = 7$ 的x的值为；

(3)、试求 $| x - 1 | + | x - 2 | + | x - 3 | + \dots + | x - 100 |$ 的最小值.

查看试题解析