初中数学苏科版七年级上学期期末复习专题10 图形的展开与折叠
试卷更新日期:2020-12-27 类型:复习试卷
一、单选题
-
1. 下列几何体的侧面展开图形状不是矩形的是( )A、圆柱 B、圆锥 C、正方体 D、棱柱2. 如图是正方体的平面展开图,则与“梅”字相对的字是( )
 A、侨 B、香 C、牛 D、旺3. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、
A、侨 B、香 C、牛 D、旺3. 下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )A、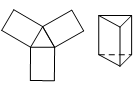 B、
B、 C、
C、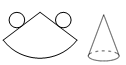 D、
D、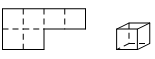 4. 已知某多面体的平面展开图如图所示,其中是三棱柱的有( )
4. 已知某多面体的平面展开图如图所示,其中是三棱柱的有( ) A、1个 B、2个 C、3个 D、4个5. 下图中是正方体展开图的有( )个.
A、1个 B、2个 C、3个 D、4个5. 下图中是正方体展开图的有( )个.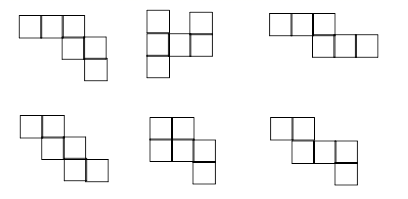 A、两个 B、三个 C、四个 D、五个6. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .
A、两个 B、三个 C、四个 D、五个6. 如图所示的三棱柱,高为 ,底面是一个边长为 的等边三角形.要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,需剪开棱的棱长的和的最小值为( ) .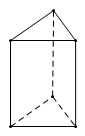 A、28 B、31 C、34 D、367. 制作一个底面直径6分米、长5分米的圆柱形通风管,至少要用( )平方分米的铁皮。A、62.8 B、94.2 C、188.4 D、565.28. 如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )
A、28 B、31 C、34 D、367. 制作一个底面直径6分米、长5分米的圆柱形通风管,至少要用( )平方分米的铁皮。A、62.8 B、94.2 C、188.4 D、565.28. 如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )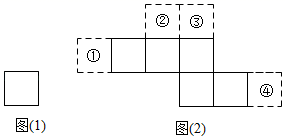 A、① B、② C、③ D、④9. 如图,正方形纸盒的底面和侧面的下半部分涂有黑色漆,将它展开得到的表面展开图是( )
A、① B、② C、③ D、④9. 如图,正方形纸盒的底面和侧面的下半部分涂有黑色漆,将它展开得到的表面展开图是( ) A、
A、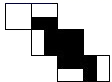 B、
B、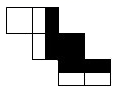 C、
C、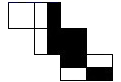 D、
D、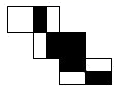 10. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )
10. 明明用纸(如图)折成了一个正方体的盒子,里面装了一瓶墨水,与其它空盒子混放在一起,只凭观察,选出墨水在哪个盒子中( )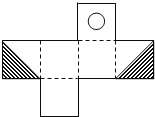 A、
A、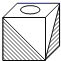 B、
B、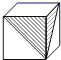 C、
C、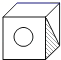 D、
D、
二、填空题
-
11. 第一行的平面图形经过折叠后能对应得到第二行的几何体,请你在横线上把它们的序号对应写出来 .
 12. 如图所示,这个图形经过折叠后能拼成一个立体图形,则该立体图形的名称是.
12. 如图所示,这个图形经过折叠后能拼成一个立体图形,则该立体图形的名称是.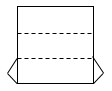 13. 把如图折成正方体后,如果相对面所对应的值相等,那么 .
13. 把如图折成正方体后,如果相对面所对应的值相等,那么 .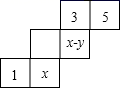 14. 如图,若要使图中平面展开图折叠成正方体后,相对面上两个数字和为6,则|x+y|= .
14. 如图,若要使图中平面展开图折叠成正方体后,相对面上两个数字和为6,则|x+y|= . 15. 长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .16. 如图一个六棱柱模型的底面边长都是5cm,侧棱长是4cm,这个六棱柱的侧面积之和是cm。
15. 长方体纸盒的长、宽、高分别是 ,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .16. 如图一个六棱柱模型的底面边长都是5cm,侧棱长是4cm,这个六棱柱的侧面积之和是cm。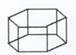 17. 已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 .
17. 已知一个圆柱的侧面展开图是如图所示的矩形,长为6π,宽为4π,那么这个圆柱底面圆的半径为 . 18. 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位: ).则此长方体包装盒的体积是.
18. 某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位: ).则此长方体包装盒的体积是.
三、解答题
-
19. 如图所示的长方形是圆柱的侧面展开图,如果这个长方形相邻的两边长分别为6, ,求圆柱体的体积.
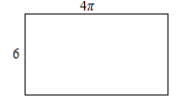 20. 某产品的形状是长方体,长为 ,它的展开图如图所示,求长方体的体积.
20. 某产品的形状是长方体,长为 ,它的展开图如图所示,求长方体的体积. 21. 解答题(1)、
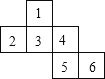
21. 解答题(1)、如图:是有一些相同小正方体搭建而成的几何体的俯视图,其中小正方形中的数字表示在这个位置小立方体的个数,请画出该几何体的主视图与左视图.
 (2)、
(2)、已知a、b互为相反数,c、d互为倒数,m的绝对值等于2,p是数轴上到原点的距离为1的数,求:p﹣cd+
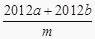 的值.22.
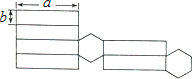
的值.22.如图,是一个几何体的侧面展开图.
(1)请写出这个几何体的名称;
(2)请根据图中所标的尺寸,计算这个几何体的侧面积.
 23. 如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题:
23. 如图所示是一个长方体的展开图,每个面上都标注了字母,请根据要求回答问题: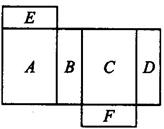 (1)、如果面A在多面体的上面,那么哪一面会在下面?(2)、如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面?(3)、从右面看是面A,从上面看是面E,那么哪一面会在前面?24. 在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30cm、宽20cm、高18cm,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
(1)、如果面A在多面体的上面,那么哪一面会在下面?(2)、如果面F在多面体的后面,从左面看是面B,那么哪一面会在上面?(3)、从右面看是面A,从上面看是面E,那么哪一面会在前面?24. 在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30cm、宽20cm、高18cm,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
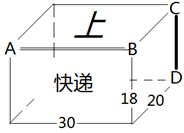
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
25.如图①所示是一个长方体盒子,四边形ABCD是边长为a的正方形,DD′的长为b.
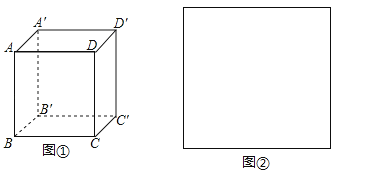
(1)写出与棱AB平行的所有的棱。
(2)求出该长方体的表面积(用含a、b的代数式表示);
(3)当a=40cm,b=20cm时,工人师傅用边长为c的正方形纸片(如图②)裁剪成六块,作为长方体的六个面,粘合成如图①所示的长方体.
①求出c的值;
②在图②中画出裁剪线的示意图,并标注相关的数据.
26.小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
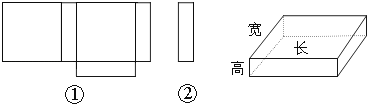
(1)小明总共剪开了 条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.