初中数学苏科版七年级上学期期末复习专题9 图形的运动
试卷更新日期:2020-12-27 类型:复习试卷
一、单选题
-
1. 下列现象,能说明“线动成面”的是( )A、天空划过一道流星 B、汽车雨刷在挡风玻璃上刷出的痕迹 C、抛出一块小石子,石子在空中飞行的路线 D、旋转一扇门,门在空中运动的痕迹2. 下列说法不正确的是( )A、四棱柱是长方体 B、八棱柱有10个面 C、六棱柱有12个顶点 D、经过棱柱的每个顶点有3条棱3. 下列说法,不正确的是( )A、用一个平面去截长方体,截面可能是正方形 B、用一个平面去截正方体,截面可能是等腰梯形 C、用一个平面去截圆锥,截面可能是梯形 D、用一个平面去截正方体,截面可能是等边三角形4.
如图所示,则图中三角形的个数一共是( )
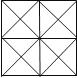 A、16 B、32 C、40 D、445. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、
A、16 B、32 C、40 D、445. 用一个平面去截一个几何体,截面不可能是圆的几何体的是( )A、 B、
B、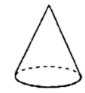 C、
C、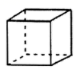 D、
D、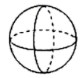 6. 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )
6. 圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是( )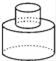 A、
A、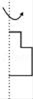 B、
B、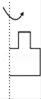 C、
C、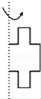 D、
D、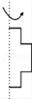 7. 如图, 是直角三角形 的高,将直角三角形 按以下方式旋转一周可以得到右侧几何体的是( ).
7. 如图, 是直角三角形 的高,将直角三角形 按以下方式旋转一周可以得到右侧几何体的是( ). A、绕着 旋转 B、绕着 旋转 C、绕着 旋转 D、绕着 旋转8. 如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个.
A、绕着 旋转 B、绕着 旋转 C、绕着 旋转 D、绕着 旋转8. 如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有( )个.①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
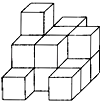
 A、1 B、2 C、3 D、49. 某学校设计了如图的一个雕塑,现在工人师傅打算用油漆喷刷所有的暴露面.经测量,已知每个小正方块的棱长均为1 m,则需喷刷油漆的总面积为( )m2
A、1 B、2 C、3 D、49. 某学校设计了如图的一个雕塑,现在工人师傅打算用油漆喷刷所有的暴露面.经测量,已知每个小正方块的棱长均为1 m,则需喷刷油漆的总面积为( )m2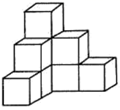 A、9 B、19 C、34 D、2910. 如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
A、9 B、19 C、34 D、2910. 如图的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的小正方体组成的,那么长方体中,第四部分所对应的几何体应是( )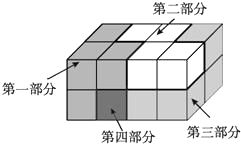 A、
A、 B、
B、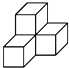 C、
C、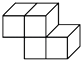 D、
D、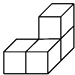
二、填空题
-
11. 用一个平面去截一个几何体,截面形状为三角形,则这个几何体可能为:①正方体;②三棱锥;③圆柱;④圆锥 (写出所有正确结果的序号).12. 长为4,宽为2的矩形绕其一边旋转构成一个圆柱的最大体积为(结果保留π).13. 如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体的体积为cm3 . (结果保留π)

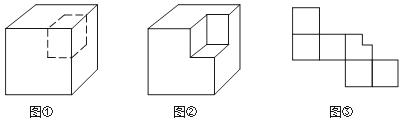
14. 用8个棱长3厘米的立方体拼成一个长方体,其中表面积最小的长方体的面积为平方厘米.15. 如图,一个 5 ´ 5 ´ 5 的正方体,先在它的前后方向正中央开凿一个“十字形”的孔(打通),再在它的上 下方向正中央也开凿一个“十字形”的孔(打通),最后在它的左右方向正中央开凿一个“十字形”的孔(打通),这样得到一个被凿空了的几何体,则凿掉部分的体积为. 16. 从棱长为2cm的正方体毛坯的一角,挖去一个棱长为1cm的小正方体,得到一个如图所示的零件,则这个零件的表面积是cm2。
16. 从棱长为2cm的正方体毛坯的一角,挖去一个棱长为1cm的小正方体,得到一个如图所示的零件,则这个零件的表面积是cm2。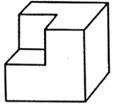 17. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.
17. 用棱长是1cm的小正方体组成如图所示的几何体,把这个几何体放在桌子上,并把暴露的面涂上颜色,那么涂颜色面的面积之和是cm2.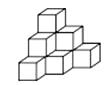 18. 李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为 .
18. 李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为 .
三、解答题
-
19.
图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.
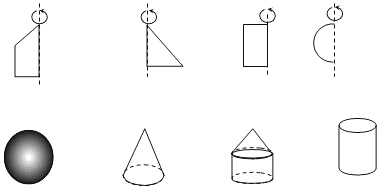 20. 已知长方形的长为5cm , 宽为4cm , 将其绕它的一边所在的直线旋转一周,得到一个立体图形.
20. 已知长方形的长为5cm , 宽为4cm , 将其绕它的一边所在的直线旋转一周,得到一个立体图形.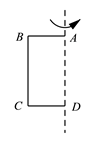 (1)、得到的几何图形的名称为 , 这个现象用数学知识解释为 .(2)、求此几何体的表面积;(结果保留π)(3)、求此几何体的体积.(结果保留π)21.
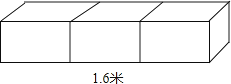
(1)、得到的几何图形的名称为 , 这个现象用数学知识解释为 .(2)、求此几何体的表面积;(结果保留π)(3)、求此几何体的体积.(结果保留π)21.如图所示,木工师傅把一个长为1.6米的长方体木料锯成3段后,表面积比原来增加了80cm2 , 那么这根木料本来的体积是多少?
 22. 在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体= , V圆锥=h)
22. 在直角三角形,两条直角边分别为6cm,8cm,斜边长为10cm,若分别以一边旋转一周(①结果用π表示;②你可能用到其中的一个公式,V圆柱=πr2h,V球体= , V圆锥=h)(1)如果绕着它的斜边所在的直线旋转一周形成的几何体是?
(2)如果绕着它的直角边6所在的直线旋转一周形成的几何体的体积是多少?
(3)如果绕着它的斜边10所在的直线旋转一周形成的几何体的体积与绕着直角边8所在的直线旋转一周形成的几何体的体积哪个大?
23. 有3个棱长分别是3cm,4cm,5cm的正方体组合成如图所示的图形.其露在外面的表面积是多少?(整个立体图形摆放在地上) 24. 观察下图并按要求回答问题。
24. 观察下图并按要求回答问题。 (1)、如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.
(1)、如图,(1)、(2)、(3)、(4)为四个平面图形,请数一数:每个平面图形各有多少个顶点?多少条边?它们分别围成了多少个区域?请你将结果填入下表.图形
顶点数
边数
区域数
(1)
4
6
3
(2)
(3)
(4)
(2)、观察上表,推断一个平面图形的顶点数,边数,区域数之间有什么关系?