辽宁省沈阳市郊联体2020-2021学年高三上学期数学期中考试试卷
试卷更新日期:2020-12-25 类型:期中考试
一、单选题
-
1. 已知集合 , ,则 ( )A、{2} B、 C、 D、2. 若复数 是纯虚数,则 ( )A、3 B、5 C、 D、3. 在△ABC中,能使sin A> 成立的充分不必要条件是( )A、A∈ B、A∈ C、A∈ D、A∈4. 边长为6的等边 中, 是线段 上的点, ,则 ( )A、48 B、30 C、24 D、125. 已知等比数列 满足 , ,则 ( )A、21 B、42 C、63 D、846. 函数 的图象大致为( )A、
 B、
B、 C、
C、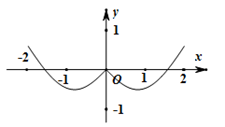 D、
D、 7. 已知 是定义域为 的奇函数,且对任意实数 ,都有 ,则 的取值范围是( )A、 B、 C、 D、8. 已知曲线 ,P为曲线C上任意一点,设曲线C在点P处的切线的倾斜角为α,则α的取值范围是( )A、 B、 C、 D、
7. 已知 是定义域为 的奇函数,且对任意实数 ,都有 ,则 的取值范围是( )A、 B、 C、 D、8. 已知曲线 ,P为曲线C上任意一点,设曲线C在点P处的切线的倾斜角为α,则α的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 下列说法中正确的有( )A、不等式 恒成立 B、存在a,使得不等式 成立 C、若 ,则 D、若正实数x,y满足 ,则10. 函数 在一个周期内的图象如图所示,则( )
 A、该函数的解析式为 B、该函数的对称中心为 C、该函数的单调递增区间是 D、把函数 的图象上所有点的横坐标变为原来的 ,纵坐标不变,可得到该函数图象11. 已知平面向量 , , 满足 .若 ,则 的值可能为( )A、 B、-2 C、0 D、12. 已知函数 ,若函数 有4个零点,则 的可能的值为( )A、 B、 C、 D、
A、该函数的解析式为 B、该函数的对称中心为 C、该函数的单调递增区间是 D、把函数 的图象上所有点的横坐标变为原来的 ,纵坐标不变,可得到该函数图象11. 已知平面向量 , , 满足 .若 ,则 的值可能为( )A、 B、-2 C、0 D、12. 已知函数 ,若函数 有4个零点,则 的可能的值为( )A、 B、 C、 D、三、填空题
-
13. 已知 , ,其中 , 是互相垂直的单位向量,则 .14. 等差数列 的前 项和为 , , ,则数列 的前50项的和为:.15. 已知函数 是定义在 上的奇函数,且满足 ,又当 时, ,则 的值等于.16. 自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“岱宗夫如何?齐鲁青未了.造化钟神秀,阴阳割昏晓,荡胸生层云,决毗入归鸟.会当凌绝顶,一览众山小.”然而,随着技术手段的发展,山高路远便不再阻碍人们出行,伟大领袖毛主席曾作词:“一桥飞架南北,天堑变通途”.在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等.如图为某工程队将 到 修建一条隧道,测量员测得一些数据如图所示( , , , 在同一水平面内),则 , 间的距离为.

四、解答题
-
17. 的内角A , B , C的对边分别为a , b , c.已知 .(1)、求角C;(2)、若 , ,求 的周长.18. 已知数列 的前 项和为 ,且 ,在等比数列 中, , .(1)、求 与 的通项公式;(2)、若 中去掉 的项后余下的项按原顺序组成数列 ,求 的前20项和.19. 已知函数 , .(1)、 的周期是 ,求 ,并求 的解集;(2)、已知 , , , ,求 的值域.