广东省阳江市江城区2020-2021学年九年级上学期数学第三次月考试卷
试卷更新日期:2020-12-25 类型:月考试卷
一、选择题(本大题共10小题,每小题3分,共30分)
-
1. 若x=2是方程x2-x+a=0的一个根,则( )A、a=1 B、a=2 C、a=-1 D、a=-22. 若双曲线y= 位于第二、四象限,则k的取值范围是( )A、k<1 B、k≥1 C、k>1 D、k≠13. 如果两个相似三角形对应边的比为2:3,那么这两个相似三角形面积的比是( )A、2:3 B、 : C、4:9 D、8:274. 下列事件是必然事件的是( )A、明天太阳从西边升起 B、掷出一枚硬币,正面朝上 C、打开电视机,正在播放世界杯足球赛 D、任意画一个三角形,它的内角和为180°5. 若点A(3,-4)、B(-2,m)在同一个反比例函数的图象上,则m的值为( )A、12 B、-12 C、6 D、-66.
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC=( )
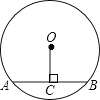 A、3cm B、4cm C、5cm D、6cm7. 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )
A、3cm B、4cm C、5cm D、6cm7. 如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是( )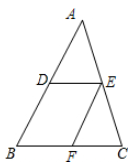 A、 B、 C、 D、8. 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到A'、B'、C的位置。若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )
A、 B、 C、 D、8. 如图,一块含有30°角的直角三角形ABC,在水平桌面上绕点C按顺时针方向旋转到A'、B'、C的位置。若BC的长为7.5cm,那么顶点A从开始到结束所经过的路径长为( )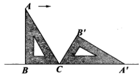 A、10πcm B、10 πcm C、15πcm D、20π9. 已知等边三角形的外接圆半径为2,则该等边三角形的边长是( )A、2 B、4 C、 D、210. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( )
A、10πcm B、10 πcm C、15πcm D、20π9. 已知等边三角形的外接圆半径为2,则该等边三角形的边长是( )A、2 B、4 C、 D、210. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=cx在同一坐标系内的大致图象是( )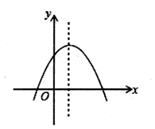 A、
A、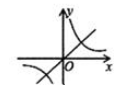 B、
B、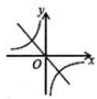 C、
C、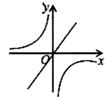 D、
D、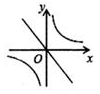
二、填空题(本大题共7小题,每小题4分,共28分)
-
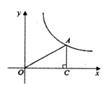
11. 已知y=(a-1)xa是反比例函数,则a的值是。12. 如图,在平面直角坐标系xOy中,点A在函数y= (x>0)的图象上,AC⊥x轴于点C,连接OA,则△OAC面积为 。
 13. 抛物线y=3(x-2)2+3的顶点坐标是。14. 已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同。若随机从中摸出一个,摸到红球的概率是 ,则袋中球的总个数是个。15. 如图,四边形ABCD是00的内接四边形,若∠C=140° ,则∠BOD=°
13. 抛物线y=3(x-2)2+3的顶点坐标是。14. 已知袋中有若干个球,其中只有2个红球,它们除颜色外其它都相同。若随机从中摸出一个,摸到红球的概率是 ,则袋中球的总个数是个。15. 如图,四边形ABCD是00的内接四边形,若∠C=140° ,则∠BOD=°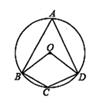 16. 如图,将半径为6的半圆,绕点A逆时针旋转75°,使点B落到点B'处,则图中阴影部分的面积是。
16. 如图,将半径为6的半圆,绕点A逆时针旋转75°,使点B落到点B'处,则图中阴影部分的面积是。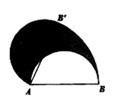 17. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”如图分别是当a=-1,a=0,a=1, a=2时二次函数的图象。它们的顶点在一条直线上, 这条直线的解析式是。
17. 已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,其图象构成一个“抛物线系”如图分别是当a=-1,a=0,a=1, a=2时二次函数的图象。它们的顶点在一条直线上, 这条直线的解析式是。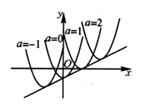
三、解答题(一) (本大题共3小题,每小题6分,共18分)
-
18. 关于x的一元二次方程x2+2x+2k-4=0有两个不相等的实数根。(1)、求k的取值范围;(2)、若方程的一个根为2,求另一个根。19. 小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20 (单位:元)的4件奖品。
 (1)、如果随机翻1张牌,那么抽中20元奖品的概率为(2)、如果随机翻2张牌,且第-次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?20.
(1)、如果随机翻1张牌,那么抽中20元奖品的概率为(2)、如果随机翻2张牌,且第-次翻过的牌不再参加下次翻牌,则所获奖品总值不低于30元的概率为多少?20.如图,一次函数y=x+m的图象与反比例函数y=的图象相交于A(2,1),B两点.
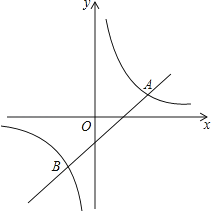 (1)、求出反比例函数与一次函数的表达式(2)、请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围
(1)、求出反比例函数与一次函数的表达式(2)、请直接写出B点的坐标,并指出使反比例函数值大于一次函数值的x的取值范围四、解答题(二) (本大题共3小题,每小题8分,共24分)
-
21. 如图,正方形ABCD中,M为BC上一点,点F是AM的中点,EF⊥AM,垂足为点F,交AD的延长线于点E,交DC于点N。
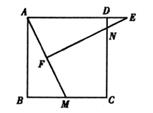 (1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长。22.
(1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长。22.环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
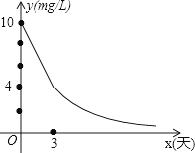 (1)、求整改过程中硫化物的浓度y与时间x的函数表达式;(2)、该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?23. 如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F。
(1)、求整改过程中硫化物的浓度y与时间x的函数表达式;(2)、该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?23. 如图,△ABC内接于⊙O,AB=AC,∠BAC=36°,过点A作AD∥BC,与∠ABC的平分线交于点D,BD与AC交于点E,与⊙O交于点F。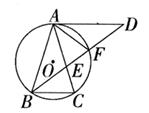 (1)、求∠DAF的度数;(2)、求证:AE2=EF·ED;
(1)、求∠DAF的度数;(2)、求证:AE2=EF·ED;五、解答题(三) (本大题共2小题,每小题10分,共20分)
-
24. 如图,直线y=2x与反比例函数y= (k≠0,x>0)的图象交于点A(m,8),AB⊥x轴,垂足为B。
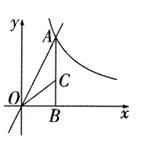 (1)、求k的值;(2)、点C在AB上,若OC=AC,求AC的长;(3)、点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD , 求点D的坐标。25. 如图①,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2 cm/s。以AQ、PQ为边作四边形AQPD,连接DQ,交AB于点E,设运动的时间为t(单位: s)(0<t≤4),解答下列问题:
(1)、求k的值;(2)、点C在AB上,若OC=AC,求AC的长;(3)、点D为x轴正半轴上一点,在(2)的条件下,若S△OCD=S△ACD , 求点D的坐标。25. 如图①,已知Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2 cm/s。以AQ、PQ为边作四边形AQPD,连接DQ,交AB于点E,设运动的时间为t(单位: s)(0<t≤4),解答下列问题: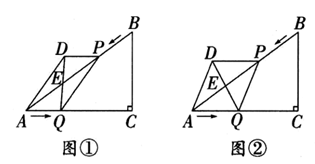 (1)、用含有t的代数式表示AE=;(2)、如图②,当t为何值时,四边形AQPD为菱形;(3)、求运动过程中,四边形AQPD的面积的最大值。
(1)、用含有t的代数式表示AE=;(2)、如图②,当t为何值时,四边形AQPD为菱形;(3)、求运动过程中,四边形AQPD的面积的最大值。