安徽省2020-2021学年九年级上学期数学第三次月考试卷
试卷更新日期：2020-12-25 类型：月考试卷
一、选择题(本大题共10小题，每小题4分，满分40分，每小题都给出A、B、C、D四个选项，其中只有一个是正确的)
-
1. 若关于x的一元二次方程x2+2x+m-1=0有一个根是0，则m的值为（ ）A、1 B、-1 C、2 D、02. 下列图形中，不是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列成语所描述的事件是随机事件的是（ ）A、水中捞月 B、旭日东升 C、不期而遇 D、海枯石烂4. 已知⊙O的半径为4cm，点P在⊙O上，则OP的长为（ ）A、2cm B、4cm C、6cm D、8cm5. 如图，AB是⊙O的直径，AC是⊙O的切线，A为切点，BC与⊙O交于点D，连接OD。若∠AOD=80°，则∠C的度数为（ ）
A、40° B、50° C、60° D、80°6. 如图是一次数学活动课上制作的两个转盘，甲转盘被平均分为三部分，上面分别写着9，8，5三个数字，乙转盘被平均分为四部分，上面分别写着1，6，9，8四个数字，同时转动两个转盘，停止转动后两个转盘上指针所指的数字恰好都能被3整除的概率是（ ）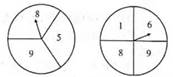
A、 B、 C、 D、7. 有两把不同的钥匙和三把锁，其中两把钥匙分别能打开两把锁，且不能打开第三把锁，随机取出一把钥匙开任意一把锁，一次打开锁的概率是（ ）A、 B、 C、 D、8. 如图．抛物线y=ax2+bx+c(a≠0)经过点(-1，0)，与y轴交于点(0，2)，抛物线的对称轴为直线x=1，下列结论：①a+c=b：②方程ax2+bx+c=0的解为-1和3；③2a+b=0；④abc<0；其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个9. 中国美食讲究色香味美，优雅的摆盘造型也会让美食錦上添花。图1中的摆盘，其形状是扇形的一部分，图2是其几何示意图(阴影部分为摆盘)，通过测量得到AC=BD=12cm，C，D两点之间的距离为4cm，圆心角为60°，则图中摆盘的面积是（ ）
A、80π cm2 B、40π cm2 C、24π cm2 D、2π cm210. 如图，PA，PB为⊙O的切线，切点分别为A，B，PO交AB于点C，PO的延长线交⊙O于点D。下列结论不一定成立的是（ ）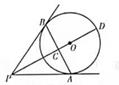
A、△BPA为等腰三角形 B、AB与PD相互垂直平分 C、点A，B都在以PO为直径的圆上 D、PC为△BPA的边AB上的中线二、填空题(本大题共4小题，每小题5分，满分20分)
-
11. 公司10月份生产64万件产品，要使12月份的产品产量达到81万件，设平均每月增长的百分率是x，则可列方程为 。12. 如图，⊙O的直径AB=2，C是半圆上任意一点，∠BCD=60°，则劣弧AD的长为。
13. 某校九年级二班举办主题演讲比赛活动．经过初赛，共有2名男生，3名女生进入决赛．决赛采用随机抽签方式确定选手的出场顺序，前两位出场的选手中，都是男选手的概率是。14. 在锐角△ABC中，AB=4，BC=5，∠ACB=45，将△ABC绕点B按逆时针方向旋转，得到△A1BC1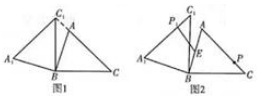
(1)、如图1，当点C1在线段CA的延长线上时，则∠CC1A1的度数为；(2)、如图2，点E为线段AB的中点，点P是线段AC．上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1 ， 则线段EP1长度的最小值是。三、(本大题共2小题，每小题8分，满分16分)
-
15. 解方程．(1)、x2-4x-12=0；(2)、x2+15=8x，16. 亮亮有3张扑克牌．冬冬有2张扑克牌，扑克牌上的数字如图所示。两人用这些扑克牌做游戏，他们先分别从自己的扑克牌中随机抽取一张，然后将他们抽出这两张扑克牌上的数字比较大小，数字大的一方获胜。请用画树状图或列表的方法，求亮亮获胜的概率。
四、(本大题共2小题，每小题8分，满分16分)
-
17. 关于x的一元二次方程x2+(2m+1)x+m2-1=0有两个实数根。(1)、求m的取值范围；(2)、写出一个m的值，使得该方程有两个不相等的实数根，并求此时方程的根。18. 如图，已知AB是⊙O的直径，弦CD⊥AB于点E，∠C=30°，OC=2。
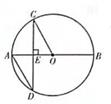(1)、求∠ADC的度数；(2)、求弦CD的长。五、(本大题共2小题，每小题10分，滿分20分)
-
19. 如图，在△ABC中，∠ACB=30°，将△ABC绕点A逆时针旋转60°，得到△ADE，连接CD，CE。
(1)、求证：AB= CD；(2)、若BC=10，∠ABC=45°，连接BE，求△BCE的面积。20. 某校举行数学竞赛活动，晓晨和阿进两位同学得分相同，获并列第一名，于是每人可在准备好的2件奖品中获得其中一件，为了决定谁先选择奖品，并同时检验学生所学的数学知识，某位数学老师设计了一个趣味性游戏，游戏规则为：将如图1所示的四张扑克牌(方块2、黑桃4、黑桃5、梅花5)洗匀后，背面朝上放置在桌面上，晓晨从中随机抽取一张，记下牌面数字；如图2是一枚质地均匀的正方休骰子，六个面分别标有点数1，2，3，4，5，6，阿进掷一次骰子，记下骰子朝上一面的点数；若晓晨记下的牌面数字大于阿进记下骰子的点数，则晓晨先挑取奖品，否则，阿进先挑取奖品。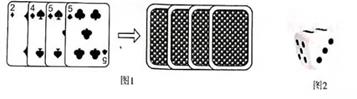
(1)、晓晨从四张扑克牌中随机抽取一张，牌面数字是5的概率是多少？(2)、请用画树状图或列表的方法说明这个游戏对双方公平吗？六、(本题满分12 分)
-
21. “绿水青山就是金山银山”的理念已融入人们的日常生活中，因此，越来越多的人喜欢骑自行车出行，某自行车店在销售某型号自行车时，标价1500元已知拔标价九折销售该型号自行车8辆与将标价直降100元销售7辆获利相同。(1)、求该型号自行车的进价是多少元？(2)、若该型号自行车的进价不变，按标价出售，该店平均每月可售出60辆；若每辆自行车每降价50元，每月可多售出10辆，求该型号自行车降价多少元时，每月犹利最大？最大利润是多少？
七、(本题满分12分)
-
22. 如图，在平面直角坐标系中，A(-1，4)，B(-4，0)，C(- 1，0)。
⑴△A1B1C1与△ABC关于原点O对称，画出△A1B1C1并写出点A1的坐标；
⑵△A2B2C2是OABC绕原点O顺时针旋转90°得到的，画出△A2B2C2并写出点A2的坐标；
⑶连接OA，OA2 ， 在△ABC绕原点O顺时针旋转90°得到△A2B2C2的过程中，计算点A变换到点A2过程中的路径是多少？ (直接写出答案)
八、(本题满分14分)
-
23. 如图1，在⊙O中，AB为⊙O的直径，点C为⊙O上一点，∠CAB=30°，过点C作⊙O的切线，与AB的延长线相交于点P。
(1)、求，∠P的度数；(2)、如图2，过点B作CP的垂线，垂足为点E与AC的延长线交于点F。①求∠F的度数；
②若⊙O的半径为2，求AF的长。
-
-