天津市滨海新区汉沽2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-25 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( )A、
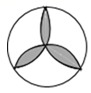 B、
B、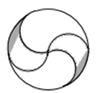 C、
C、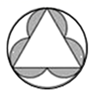 D、
D、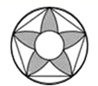 2. 抛物线 的顶点坐标是( )A、 B、 C、 D、3. 关于 的一元二次方程 根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定4. 方程 的解是( )A、 B、 C、 , D、 ,5. 如图,⊙O的直径AB过弦CD的中点E , ∠COB=40°,则∠BAD等于( )
2. 抛物线 的顶点坐标是( )A、 B、 C、 D、3. 关于 的一元二次方程 根的情况是( )A、有两个不等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定4. 方程 的解是( )A、 B、 C、 , D、 ,5. 如图,⊙O的直径AB过弦CD的中点E , ∠COB=40°,则∠BAD等于( )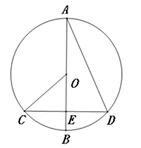 A、80° B、50° C、40° D、20°6. 把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )A、y=3(x+3)2﹣2 B、y=3(x+3)2+2 C、y=3(x﹣3)2﹣2 D、y=3(x﹣3)2+27. 如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后得到 ,如果AP=2,那么 的长等于( )
A、80° B、50° C、40° D、20°6. 把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得的抛物线是( )A、y=3(x+3)2﹣2 B、y=3(x+3)2+2 C、y=3(x﹣3)2﹣2 D、y=3(x﹣3)2+27. 如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后得到 ,如果AP=2,那么 的长等于( )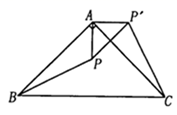 A、 B、 C、 D、48. 如果a是一元二次方程 的一个根, 是一元二次方程 的一个根,那么a的值等于( )A、1或2 B、0或3 C、-1或-2 D、09. 抛物线 的对称轴在 轴右侧,则 的取值范围是( )A、 B、 C、 D、10. 参加足球联赛的每两队之间都进行两场比赛(这样的比赛叫做双循环比赛),共要比赛90场.设有 个球队参加比赛,根据题意,列出方程为( )A、 B、 C、 D、11. 如图,MN是 的直径,点A是半圆上一个三等分点,点B是 的中点,点 是点B关于MN的对称点, 的半径为1,则 的长等于( )
A、 B、 C、 D、48. 如果a是一元二次方程 的一个根, 是一元二次方程 的一个根,那么a的值等于( )A、1或2 B、0或3 C、-1或-2 D、09. 抛物线 的对称轴在 轴右侧,则 的取值范围是( )A、 B、 C、 D、10. 参加足球联赛的每两队之间都进行两场比赛(这样的比赛叫做双循环比赛),共要比赛90场.设有 个球队参加比赛,根据题意,列出方程为( )A、 B、 C、 D、11. 如图,MN是 的直径,点A是半圆上一个三等分点,点B是 的中点,点 是点B关于MN的对称点, 的半径为1,则 的长等于( ) A、1 B、 C、 D、12. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ( 为任意实数).其中正确的个数为( )
A、1 B、 C、 D、12. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 .下列说法:① ;② ;③ ( 为任意实数).其中正确的个数为( )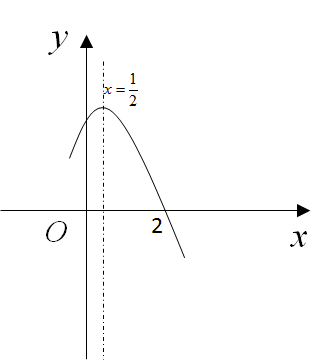 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 若关于 的方程 是一元二次方程,则 满足的条件是 .14. 把方程 化为一元二次方程的一般形式,其结果是 .15. 如图,在⊙ 中,弦 与直径 相交于点 , .则 的大小等于 .
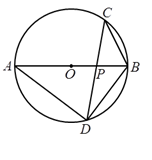 16. 已知点(2,6),(4,6)是抛物线 上的两点, 则这条抛物线的对称轴是 .17. 如图,平行四边形ABCD中, ,点 的坐标是 ,以点 为顶点的抛物线经过 轴上的点A , B , 则此抛物线的解析式为 .
16. 已知点(2,6),(4,6)是抛物线 上的两点, 则这条抛物线的对称轴是 .17. 如图,平行四边形ABCD中, ,点 的坐标是 ,以点 为顶点的抛物线经过 轴上的点A , B , 则此抛物线的解析式为 .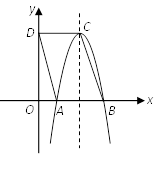 18. 在 中, ,将 绕顶点 顺时针旋转得到 ,点 是 的中点,点 是 的中点,连接 .若 , ,则在旋转一周的过程中线段 长度的最大值等于 .
18. 在 中, ,将 绕顶点 顺时针旋转得到 ,点 是 的中点,点 是 的中点,连接 .若 , ,则在旋转一周的过程中线段 长度的最大值等于 .
三、解答题
-
19. 解方程:(1)、 ;(2)、 .20. 已知抛物线 的对称轴是直线 ,此抛物线与 轴交于 、 两点,与 轴交于点 .(1)、求 的面积;(2)、若抛物线的顶点为 ,求线段 的长.21. 如图,在平面直角坐标系中,点 ,点 在第一象限, , ,将 绕点 按逆时针方向旋转 得到 ,连接 .
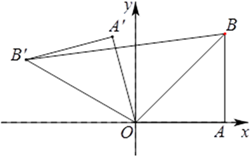 (1)、求 的度数;(2)、求出点 的坐标.22. 已知, 为⊙ 的直径, , 为⊙ 上一点, 为 的中点,连接 .
(1)、求 的度数;(2)、求出点 的坐标.22. 已知, 为⊙ 的直径, , 为⊙ 上一点, 为 的中点,连接 .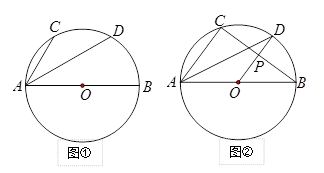 (1)、如图①,若 ,求 的长;(2)、如图②,若 , 与 相交于点 ,求 、 的长.23. 某旅行社为吸引市民组团去某新开发的风景区旅游,推出了如下收费标准:如果旅游团人数不超过25人,人均旅游费用为1000元;如果旅游团人数超过25人,每增加1人,人均旅游费用降低20元,但人均旅游费用不得低于700元.设旅游团人数为 人.(1)、写出支付给旅行社费用 y (单位:元)关于 x 的函数关系式;(2)、某单位组织员工组团去此风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少人去旅游?
(1)、如图①,若 ,求 的长;(2)、如图②,若 , 与 相交于点 ,求 、 的长.23. 某旅行社为吸引市民组团去某新开发的风景区旅游,推出了如下收费标准:如果旅游团人数不超过25人,人均旅游费用为1000元;如果旅游团人数超过25人,每增加1人,人均旅游费用降低20元,但人均旅游费用不得低于700元.设旅游团人数为 人.(1)、写出支付给旅行社费用 y (单位:元)关于 x 的函数关系式;(2)、某单位组织员工组团去此风景区旅游,共支付给旅行社旅游费用27000元,请问该单位这次共有多少人去旅游?