山西省吕梁市交城县2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-25 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、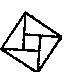 C、
C、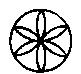 D、
D、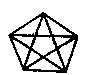 3. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、4. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、
3. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、4. 如图,函数 和 ( 是常数,且 )在同一平面直角坐标系的图象可能是( )A、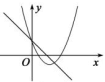 B、
B、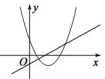 C、
C、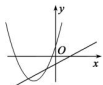 D、
D、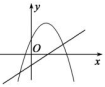 5. 三角形两边长分别是8和6,第三边长是一元二次方程x2﹣16x+60=0一个实数根,则该三角形的面积是( )A、24 B、48 C、24或8 D、86. 如图,把一个直角三角板△ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BDC的度数为( )
5. 三角形两边长分别是8和6,第三边长是一元二次方程x2﹣16x+60=0一个实数根,则该三角形的面积是( )A、24 B、48 C、24或8 D、86. 如图,把一个直角三角板△ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合,连接CD,则∠BDC的度数为( ) A、15° B、20° C、25° D、30°7. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、8. 如图,在长为100米,宽为80米的矩形场地上修建两条小路,剩余部分进行绿化,要使绿化面积为7644平方米,那么小路进出口的宽度应为多少米?设小路进出口的宽为x米,则可列方程为( )(注:所有小路进出口的宽度都相等,且每段小路均为平行四边形)
A、15° B、20° C、25° D、30°7. 将抛物线 向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线解析式为( )A、 B、 C、 D、8. 如图,在长为100米,宽为80米的矩形场地上修建两条小路,剩余部分进行绿化,要使绿化面积为7644平方米,那么小路进出口的宽度应为多少米?设小路进出口的宽为x米,则可列方程为( )(注:所有小路进出口的宽度都相等,且每段小路均为平行四边形)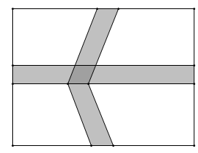 A、 B、 C、 D、9. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),与 轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )
A、 B、 C、 D、9. 如图,抛物线 的对称轴为直线 ,与 轴的一个交点坐标为(-1,0),与 轴交点为(0,3),其部分图象如图所示,则下列结论错误的是( )① ;②当 时, 随 的增大而减小;③当 时, ;④关于 的方程 有两个相等的实数根
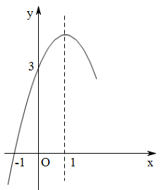 A、①③ B、②④ C、③④ D、①②④10. 如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是( )
A、①③ B、②④ C、③④ D、①②④10. 如图,AB是⊙O的直径,AB=AC且∠BAC=45°,⊙O交BC于点D,交AC于点E,DF与⊙O相切,OD与BE相交于点H.下列结论错误的是( )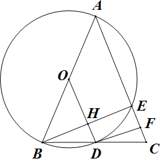 A、BD=CD B、四边形DHEF为矩形 C、 D、BC=2CE
A、BD=CD B、四边形DHEF为矩形 C、 D、BC=2CE二、填空题
-
11. 电影《我和我的家乡》首映当日票房突破2.5亿元,两天后票房达到3.6亿元,那么平均每天票房的增长率为 .12. 若关于 的一元二次方程 有两个不相等的实数根,则 满足 .13. 如图,已知二次函数 与一次函数 的图象交于点A(-2,4),B(8,2),则能使 成立的自变量 的取值范围为 .
 14. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.
14. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在弧BC上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.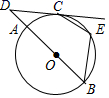 15. 如图,在Rt△ABC中,AC=4,BC=3 ,将Rt△ABC以点A为中心,逆时针旋转60°得到△ADE,则线段BE的长度为 .
15. 如图,在Rt△ABC中,AC=4,BC=3 ,将Rt△ABC以点A为中心,逆时针旋转60°得到△ADE,则线段BE的长度为 .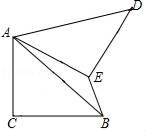
三、解答题
-
16. 解下列方程(1)、(2)、17. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
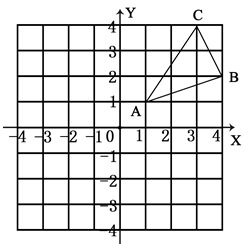 (1)、请画出△ABC向左平移5个单位长度后得到的△A1B1C1(2)、请画出△ABC关于原点对称的△A2B2C2;(3)、在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.18. 如图,已知矩形ABCD中,AD=3,对角线AC,BD的长是一元二次方程 的两个实数根.
(1)、请画出△ABC向左平移5个单位长度后得到的△A1B1C1(2)、请画出△ABC关于原点对称的△A2B2C2;(3)、在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.18. 如图,已知矩形ABCD中,AD=3,对角线AC,BD的长是一元二次方程 的两个实数根.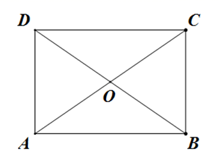 (1)、求m的值;(2)、求矩形ABCD的面积.19. 如图隧道的截面由抛物线和长方形构成,长方形的长是12m , 宽是4m . 按照图中所示的直角坐标系,抛物线可以用y= 表示,且抛物线上的点C到OB的水平距离为3m , 到地面OA的距离为 m .
(1)、求m的值;(2)、求矩形ABCD的面积.19. 如图隧道的截面由抛物线和长方形构成,长方形的长是12m , 宽是4m . 按照图中所示的直角坐标系,抛物线可以用y= 表示,且抛物线上的点C到OB的水平距离为3m , 到地面OA的距离为 m .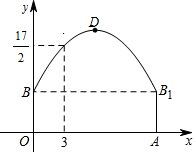 (1)、求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)、一辆货运汽车载一长方体集装箱后高为6m , 宽为4m , 如果隧道内设双向车道,那么这辆货车能否安全通过?20. 某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;(2)、一辆货运汽车载一长方体集装箱后高为6m , 宽为4m , 如果隧道内设双向车道,那么这辆货车能否安全通过?20. 某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=-x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求w与x之间的函数解析式;
(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
21. 如图,在Rt△ABC中,∠A=90°,O是BC上一点,以O为圆心,OC为半径作圆切AB于点D,交BC于点E,交AC于点F,连接CD. (1)、若∠ADC=60°,求证:∠B=∠ACD;(2)、在(1)的基础上,若AC=3,求弓形CF的面积.22. 实践与探究
(1)、若∠ADC=60°,求证:∠B=∠ACD;(2)、在(1)的基础上,若AC=3,求弓形CF的面积.22. 实践与探究已知:△ABC和△DOE都是等腰三角形,∠CAB=∠DOE=90°,点O是BC的中点,发现结论:
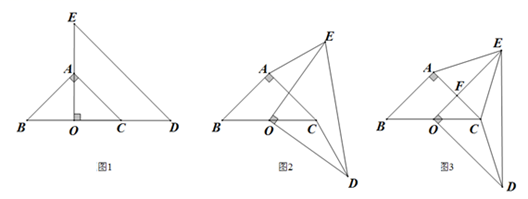 (1)、如图1,当OE经过点A,OD经过点C时,线段AE和CD的数量关系是 , 位置关系是 .(2)、在图1的基础上,将△DOE绕点O顺时针旋转 ( )得到图2,则问题(1)中的结论是否成立?请说明理由.(3)、如图3在(2)的基础上,当AE=CE时,请求出 的度数.(4)、在(2)的基础上,△DOE在旋转的过程中设AC与OE相交于点F,当△OFC为等腰三角形时,请直接写出 的度数.23. 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.
(1)、如图1,当OE经过点A,OD经过点C时,线段AE和CD的数量关系是 , 位置关系是 .(2)、在图1的基础上,将△DOE绕点O顺时针旋转 ( )得到图2,则问题(1)中的结论是否成立?请说明理由.(3)、如图3在(2)的基础上,当AE=CE时,请求出 的度数.(4)、在(2)的基础上,△DOE在旋转的过程中设AC与OE相交于点F,当△OFC为等腰三角形时,请直接写出 的度数.23. 如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.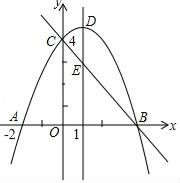 (1)、求抛物线的解析式;(2)、若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积最大,若存在,求出点F的坐标和最大值;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相较于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求P点的坐标.
(1)、求抛物线的解析式;(2)、若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积最大,若存在,求出点F的坐标和最大值;若不存在,请说明理由;(3)、平行于DE的一条动直线l与直线BC相较于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求P点的坐标.