吉林省松原市乾安县2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2020-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 如果a与2020互为相反数，那么a是（）

A、2020 B、- 2020 C、 $\frac{1}{2020}$ D、- $\frac{1}{2020}$

查看试题解析
2.
如图是加工零件的尺寸要求，现有下列直径尺寸的产品（单位：mm），其中不合格的是（）

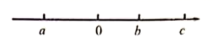
A、Φ45.02 B、Φ44.9 C、Φ44.98 D、Φ45.01

查看试题解析
3. 下列各式中运算错误的是（）

A、 $5 x - 2 x = 3 x$ B、 $5 a b - 5 b a = 0$ C、 $4 x^{2} y - 5 x y^{2} = - x^{2} y$ D、 $3 x^{2} + 2 x^{2} = 5 x^{2}$

查看试题解析
4. 小红要购买珠子串成一条手链，黑色珠子每个a元，白色珠子每个b元，要串成如图所示的手链，小红购买珠子应该花费（）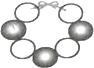

A、（3a+4b）元 B、（4a+3b）元 C、4（a+b）元 D、3（a+b）元

查看试题解析
5. 某商店举办促销活动，促销的方法是将原价x元的衣服以 $\frac{3}{5}$ （x﹣10）元出售，则下列说法中，能符合题意表达该商店促销方法的是（　　）

A、原价减去10元后再打6折 B、原价打6折后再减去10元 C、原价减去10元后再打4折 D、原价打4折后再减去10元

查看试题解析
6. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b.对于以下结论：

甲：b−a<0；乙：a+b>0；丙：|a|<|b|；丁： $\frac{b}{a}$ >0；其中正确的是（）

A、甲乙 B、丙丁 C、甲丙 D、乙丁

查看试题解析

二、填空题

7. 地球上陆地的面积约为148 000 000平方千米，用科学记数法表示为平方千米， 1.8935（用四舍五入法精确到0.001）为；566.1235精确到个位为．

查看试题解析
8. 如果一个单项式 $- \frac{a^{2} b}{2}$ 的系数和次数分别为m、n，那么 $\frac{m n}{3}$ = ．

查看试题解析
9. 如果单项式﹣xy^b+1与 $\frac{1}{2}$ x^a^﹣²y³是同类项，那么 ${(b - a)}^{2021} =$ ．

查看试题解析
10. 有理数 $a$ ， $b$ ， $c$ 在数轴上的对应点如图所示，化简： $| a + b | - | b - c | + | c - a - b | =$ ．

查看试题解析
11. 多项式 $2 x + 2 x^{2} y - 4$ 的次数是，次数最高的项是，常数项是．

查看试题解析
12. 当 $x = 1$ 时，代数式 $a x^{3} + b x + 1$ 的值2020，当 $x = - 1$ 时，代数式 $a x^{3} + b x + 1$ 的值为．

查看试题解析
13. 按照如图所示的操作步骤，若输入的值为3，则输出的值为．

查看试题解析
14. 下列图案是用长度相同的火柴棒按一定规律拼搭而成，图案①需8根火柴棒，图案②需15根火柴棒，…，按此规律，图案⑦需根火柴棒．

查看试题解析

三、解答题

15. 计算：

(1)、 $0 - (- 7) - (- 3)$

(2)、 $(- 81) \div 2 \frac{1}{4} \times \frac{4}{9} \div (- 16)$

查看试题解析
16. 已知a、b互为相反数，c、d互为倒数，m的绝对值是 $5$ ，
求： $m^{2} - \frac{2020 (a + b)}{2021} + c d$ 的值．

查看试题解析
17. 请你把 $3^{2}$ 、 ${(- 2)}^{3}$ 、|－ $\frac{1}{2}$ |、－ $\frac{1}{5}$ 、0、-（-3）、-1.5这七个数按照从小到大，从左到右的顺序串成一个糖葫芦．

查看试题解析
18. 先化简再求值： $3 (x^{2} - 2 x y) - [3 x^{2} - 2 y + 2 (2 x y + y)]$ ，其中x=-1，y =2．

查看试题解析
19. 阅读计算过程：
$3 \frac{1}{3} - 2^{2} \div [{(\frac{1}{2})}^{2} - (- 3 + 0.75)] \times 5$

解：原式 $= 3 \frac{1}{3} - 2^{2} \div [\frac{1}{4} - 3 + \frac{3}{4}] \times 5$ ①

$= 3 \frac{1}{3} + 4 \div [- 2] \times 5$ ②

$= 3 \frac{1}{3} + \frac{2}{5}$ ③

回答下列问题：（注：（1）（2）（3）问回答时用文字说明）

(1)、步骤①错在；

(2)、步骤①到步骤②错在；

(3)、步骤②到步骤③错在；

(4)、写出正确的计算过程．

查看试题解析
20. 在计算代数式（2x³－3x²y－2xy²）－（x³－2xy²+y³）+（－x³+3x²y－y³）的值，其中x=2021，y= －1时，甲同学把x=2021错抄成x= －2021，但他计算的结果是正确的．试说明理由，并求出这个结果．

查看试题解析
21. 王先生到市行政中心大楼办事，假定乘电梯向上一楼记作+1，向下一楼记作﹣1，王先生开始从1楼出发，电梯上下楼层依次记录如下（单位：层）：+6，﹣3，+10，﹣8，+12，﹣7，﹣10．

(1)、请你通过计算说明王先生最后是否回到出发点1楼；

(2)、该中心大楼每层高3m，电梯每向上或下1m需要耗电0.2度，根据王先生现在所处位置，请你算算，他办事时电梯需要耗电多少度？

查看试题解析
22. 做大小两个长方体纸盒，尺寸如下（单位：cm）

长

宽

高

小纸盒

a

b

c

大纸盒

1.5a

2b

2c

(1)、做这两个纸盒共用料多少平方厘米？（结果用含a、b、c的代数式表示）

(2)、做成的大纸盒比小纸盒多用料多少平方厘米？（结果用含a、b、c的代数式表示）

查看试题解析

23. 我国属于水资源缺乏的国家之一，节约用水，人人有责．为了强化公民的节水意识，合理利用水资源，采用价格调控手段达到节水的目的，某市自来水价格表如下：

每月用水量	单价
不超过5 $m^{3}$	3元/ $m^{3}$
超过5 $m^{3}$ 不超过10 $m^{3}$ 的部分	5元/ $m^{3}$
超过10 $m^{3}$ 的部分	8元/ $m^{3}$

注：水费按月结算

(1)、若某户居民3月份用水4

m^{3}

，则应缴水费元；

(2)、若某户居民4月份用水8

m^{3}

，求应缴水费多少元？

(3)、若某户居民8月份用水x

m^{3}

（其中x大于5），求应缴水费多少元？（用含x的式子表示）

查看试题解析

24. 观察下列三行数：
－3，9，－27，81，－243，….

－5，7，－29，79，－245，….

－1，3，－9，27，－81，….

(1)、第一行数是按什么规律排列的？

(2)、第二行、第三行数与第一行数分别有什么关系？

(3)、分别取这三行数中的第6个数，计算这三个数的和．

查看试题解析
25. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论的数学思想解决问题的过程，请仔细阅读，并解答题目后提出的探究问题.
（提出问题）三个有理数a，b，c，满足abc>0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值.

（解决问题）

解：由题意得：a，b，c三个有理数都为正数或其中一个为正数，另两个为负数.

①当a，b，c，都是整数，即a>0，b>0，c>0时，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{b}{b} + \frac{c}{c}$ =1+1+1=3；

②当a，b，c有一个为正数，另两个位负数时，设a>0，b<0，c<0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{- b}{b} + \frac{- c}{c}$ =1−1−1=−1；

所以 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或−1.

（探究）请根据上面的解题思路解答下面的问题：

(1)、三个有理数a，b，c满足abc<0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(2)、已知 $| a |$ =9， $| b |$ =4，且a<b，求a−2b的值.

查看试题解析
26. 如图所示，在数轴上点A表示的有理数为-6，点B表示的有理数为4，点P从点A出发，以每秒2个单位长度的速度在数轴上向点B运动，当点P到达点B后立即返回，仍然以每秒2个单位长度的速度运动至点A停止．设运动时间为t（单位：秒）．

(1)、求t=1时点P表示的有理数；

(2)、求点P与点B重合时的t值；

(3)、在点P沿数轴由点A到点B再回到点A的运动过程中，求点P与点A的距离（用含t的代数式表示）；

(4)、当点P表示的有理数与原点的距离是2个单位长度时，直接写出所有满足条件的t值.

查看试题解析

	长	宽	高
小纸盒	a	b	c
大纸盒	1.5a	2b	2c