上海市浦东新区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. $Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $C B = 4$ ，则 $\tan A$ 的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
2. 已知两个相似三角形的周长比为4：9，则它们的面积比为（）

A、4：9 B、2：3 C、8：18 D、16：81

查看试题解析
3. 已知 $\frac{a}{b} = \frac{3}{5}$ ，下列说法中，错误的是（）

A、 $\frac{a + b}{b} = \frac{8}{5}$ B、 $\frac{a - b}{b} = \frac{- 2}{5}$ C、 $\frac{a + 1}{b + 1} = \frac{a}{b}$ D、 $\frac{b}{a} = \frac{5}{3}$

查看试题解析
4. 已知△ABC中，D ， E分别是边BC ， AC上的点，下列各式中，不能判断DE∥AB的是（　　）

A、 $\frac{A E}{E C} = \frac{B D}{D C}$ B、 $\frac{A E}{A C} = \frac{B D}{B C}$ C、 $\frac{A C}{B C} = \frac{E C}{D C}$ D、 $\frac{D E}{A B} = \frac{C E}{A C}$

查看试题解析
5. 已知点C是线段AB的中点，下列结论中，正确的是（　　）

A、 $\vec{C A} = \frac{1}{2} \vec{A B}$ B、 $\vec{C B} = \frac{1}{2} \vec{A B}$ C、 $\vec{A C} + \vec{B C} = 0$ D、 $\vec{A C} + \vec{C B} = \vec{0}$

查看试题解析
6. 一段公路路面的坡度为i＝1：2.4．如果某人沿着这段公路向上行走了260m ，那么此人升高了（　　）

A、50m B、100m C、150m D、200m

查看试题解析

二、填空题

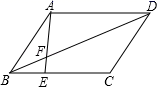
7. 如果在某建筑物的A处测得目标B的俯角为37°，那么从目标B可以测得这个建筑物的A处的仰角为．

查看试题解析
8. 已知向量 $\vec{a}$ 与单位向量 $\vec{e}$ 的方向相反，且长度为2，那么用 $\vec{e}$ 表示 $\vec{a} =$ .

查看试题解析
9. 已知点C是线段AB的黄金分割点，且AC＞BC，若AB＝2，则AC＝．

查看试题解析
10. 如果 $\vec{a} + \vec{b} = 2 \vec{c}, 2 \vec{a} - \vec{b} = 3 \vec{c}$ ，那么用 $\vec{b}$ 表示 $\vec{a}$ ．

查看试题解析
11. 已知梯形的上下两底长度为4和6，将两腰延长交于一点，这个交点到两底边的距离之比是．

查看试题解析
12. 已知在Rt△ABC中，∠C＝90°，∠A＝α，AB＝m ，那么边AB上的高为．

查看试题解析
13. 在△ABC中，AB＝5，BC＝8，∠B＝60°，则S_△_ABC＝（结果保留根号）

查看试题解析
14. 如图，在平行四边形ABCD中，点E在边BC上，EC＝2BE ，连接AE交BD于点F ，若△BFE的面积为2，则△AFD的面积为．

查看试题解析
15. 如图，已知AB⊥BD，ED⊥BD，C是线段BD的中点，且AC⊥CE，ED=1，BD=4，那么AB=.

查看试题解析
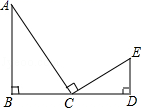16. 已知菱形ABCD的边长为6，对角线AC与BD相交于点O ， OE⊥AB ，垂足为点E ， AC＝4，那么sin∠AOE＝．

查看试题解析
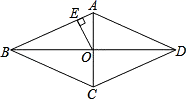17. 在平面直角坐标系xOy中，已知一次函数y＝kx+b（k≠0）的图象过点P（1，1），与x轴交于点A ，与y轴交于点B ，且tan∠ABO＝2，那么点A的坐标是．

查看试题解析
18. 如图，已知△ABC中，∠B＝90°，BC＝3，AB＝4，D是边AB上一点，DE∥BC交AC于点E ，将△ADE沿DE翻折得到△A′DE ，若△A′EC是直角三角形，则AD长为．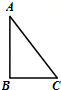

查看试题解析

三、解答题

19. 计算：cos²45° $- \frac{tan 30 °}{2 sin 60 °}$ ＋cot²30°.

查看试题解析
20. 已知如图， $A D ∥ B E ∥ C F$ ，它们依次交直线a，b于点A、B、C和点D、E、F.

(1)、如果 $A B = 6$ ， $B C = 8$ ， $D F = 21$ ，求DE的长.

(2)、如果 $D E ： D F = 2 ： 5$ ， $A D = 9$ ， $C F = 14$ ，求BE的长.

查看试题解析
21. 如图，E是平行四边形ABCD的边BA延长线上的一点，CE交AD于点F ，交BD于点G ， AE：AB＝1：3，设 $\vec{B A}$ ＝ $\vec{a}$ ， $\vec{B C}$ ＝ $\vec{b}$ ．

(1)、用向量 $\vec{a}$ 、 $\vec{b}$ 分别表示下列向量：
$\vec{A E}$ ＝， $\vec{E C}$ ＝， $\vec{E G}$ ＝；

(2)、在图中求作向量 $\vec{B G}$ 分别在 $\vec{a}$ 、 $\vec{b}$ 方向上的分向量．（不写作法，但要写出画图结果）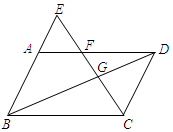

查看试题解析
22. 如图，A ， B两地之间有一座山，汽车原来从A地到B地须经C地沿折线A﹣C﹣B行驶，全长68km ．现开通隧道后，汽车直接沿直线AB行驶．已知∠A＝30°，∠B＝45°，则隧道开通后，汽车从A地到B地比原来少走多少千米？（结果精确到0.1km）（参考数据： $\sqrt{2}$ ≈1.4， $\sqrt{3}$ ≈1.7）

查看试题解析
23. 已知：如图，四边形ABCD是菱形，点E在边CD上，点F在BC的延长线上，CF＝DE ， AE的延长线与DF相交于点G ．

(1)、求证：∠CDF＝∠DAE；

(2)、如果DE＝CE ，求证：AE＝3EG ．

查看试题解析
24. 如果，已知△ABC ， A（0，﹣4），B（﹣2，0），C（4，0）．

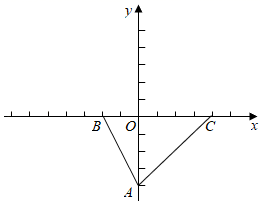(1)、求sin∠BAC的值．

(2)、若点P在y轴上，且△POC与△AOB相似，请直接写出点P的坐标．

(3)、已知点M在y轴上，如果∠OMB+∠OAB＝∠ACB ，求点M的坐标．

查看试题解析
25. 如图，已知在△ABC中，AB=AC，BC比AB大3， $\sin B = \frac{4}{5}$ ，点G是△ABC的重心，AG的延长线交边BC于点D．过点G的直线分别交边AB于点P、交射线AC于点Q.

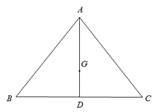(1)、求AG的长；

(2)、当∠APQ=90º时，直线PG与边BC相交于点M.求 $\frac{A Q}{M Q}$ 的值；

(3)、当点Q在边AC上时，设BP=x，AQ=y，求y关于x的函数解析式，并写出它的定义域.

查看试题解析