黑龙江省齐齐哈尔市讷河市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2020-12-24 类型:期中考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是A、
 B、
B、 C、
C、 D、
D、 2. 抛物线 的顶点坐标是( )A、(0,3) B、(3,0) C、(0,﹣3) D、(﹣3,0)3. 若关于 的一元二次方程 的常数项为0,则m的值等于( )A、1 B、2 C、1或2 D、04. 将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )A、y=(x+1)2﹣13 B、y=(x﹣5)2﹣3 C、y=(x﹣5)2﹣13 D、y=(x+1)2﹣35. 在一个有10万人的小镇,随机调查了1000人,其中有120人周六早上观看中央电视台的“朝闻天下”节目,那么在该镇随便问一个人,他在周六早上观看中央电视台的“朝闻天下”节目的概率大约是( )A、 B、 C、 D、6. 过⊙O内一点M的最长弦长为10 cm , 最短弦长为8 cm , 那么OM为( )A、6 cm B、3 cm C、 cm D、9 cm7. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
2. 抛物线 的顶点坐标是( )A、(0,3) B、(3,0) C、(0,﹣3) D、(﹣3,0)3. 若关于 的一元二次方程 的常数项为0,则m的值等于( )A、1 B、2 C、1或2 D、04. 将抛物线y=x2﹣4x﹣4向左平移3个单位,再向上平移5个单位,得到抛物线的函数表达式为( )A、y=(x+1)2﹣13 B、y=(x﹣5)2﹣3 C、y=(x﹣5)2﹣13 D、y=(x+1)2﹣35. 在一个有10万人的小镇,随机调查了1000人,其中有120人周六早上观看中央电视台的“朝闻天下”节目,那么在该镇随便问一个人,他在周六早上观看中央电视台的“朝闻天下”节目的概率大约是( )A、 B、 C、 D、6. 过⊙O内一点M的最长弦长为10 cm , 最短弦长为8 cm , 那么OM为( )A、6 cm B、3 cm C、 cm D、9 cm7. 某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )
A、200(1+x)2=1000 B、200+200×2x=1000 C、200+200×3x=1000 D、200[1+(1+x)+(1+x)2]=10008. 在同一直角坐标系中,函数y=mx+m和函数y=mx2+2x+2(m是常数,且m≠0)的图象可能是( )A、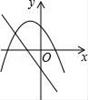 B、
B、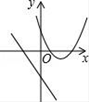 C、
C、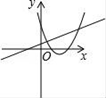 D、
D、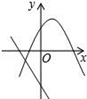 9. 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的半径为( )
9. 如图,AB为⊙O的直径,弦CD⊥AB于E,已知CD=12,BE=2,则⊙O的半径为( ) A、8 B、10 C、16 D、2010. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc<0;②b2﹣4ac>0;③a+b+c<0;④3a+c<0;其中结论正确的个数有( )
A、8 B、10 C、16 D、2010. 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc<0;②b2﹣4ac>0;③a+b+c<0;④3a+c<0;其中结论正确的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11.
如图,正五边形ABCDE内接于⊙O,则∠CAD= 度.
 12. 若关于x的函数 与x轴仅有一个公共点,则实数k的值为.13. 已知圆锥的底面半径长为3,高为4,则它的全面积是.14. 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离cm.
12. 若关于x的函数 与x轴仅有一个公共点,则实数k的值为.13. 已知圆锥的底面半径长为3,高为4,则它的全面积是.14. 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为10cm,母线OE(OF)长为10cm.在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离cm. 15. 一个半径为4cm的圆内接正六边形的面积等于cm2 .16. 如图,AB、AC与⊙O相切于点B、C,∠A=54°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 .
15. 一个半径为4cm的圆内接正六边形的面积等于cm2 .16. 如图,AB、AC与⊙O相切于点B、C,∠A=54°,P为⊙O上异于B、C的一个动点,则∠BPC的度数为 . 17. 如图,在直角坐标系中,已知点 、 ,对 连续作旋转变换,依次得到 ,则 的直角顶点的坐标为 .
17. 如图,在直角坐标系中,已知点 、 ,对 连续作旋转变换,依次得到 ,则 的直角顶点的坐标为 .
三、解答题
-
18. 已知二次函数的顶点坐标为(4,-2),且其图象经过点(5,1),求此二次函数的解析式.19. 解方程(1)、(2)、20. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C(3,5)(每个方格的边长均为1个单位长度).

⑴请画出将△ABC向下平移5个单位后得到的△A1B1C1;
⑵将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2 , 并直接写出点B旋转到点B2所经过的路径长.
21. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.(1)、若将这种水果每斤的售价降低x元,则每天的销售量是 斤。(用含x的代数式表示)(2)、销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?22. 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠CAE=∠ADC. (1)、求证:AE是⊙O的切线;(2)、若⊙O的半径为2,∠B=60°,求图中阴影部分的面积.(结果保留根号和π)23. 九(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
(1)、求证:AE是⊙O的切线;(2)、若⊙O的半径为2,∠B=60°,求图中阴影部分的面积.(结果保留根号和π)23. 九(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.男、女生所选项目人数统计表
项目
男生人数
女生人数
机器人
7
9
3D打印机
m
4
航模
2
2
其他
5
n

根据以上信息解决下列问题:
(1)、 , ;(2)、扇形统计图中机器人项目所对应扇形的圆心角度数为°;(3)、从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.24.如图,抛物线经过A(﹣1,0),B(5,0),C(0, )三点.
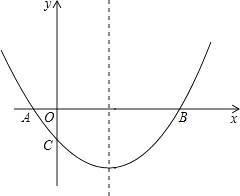 (1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)、点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.