黑龙江省齐齐哈尔市建华区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2020-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 下面服装品牌 LOGO中，是中心对称图形的为（）

A、 B、 C、 D、

查看试题解析
2. 下列事件中，必然事件是（）

A、掷一枚硬币，正面朝上 B、a是实数，︱a︱≥0 C、某运动员跳高的最好成绩是20.1米 D、从车间刚生产的产品中任意抽取一个，是次品

查看试题解析
3. 如图，⊙O的半径为1，A，B，C是圆周上的三点，∠BAC=36°，则劣弧BC的长是（）

A、 $\frac{1}{5} π$ B、 $\frac{2}{5} π$ C、 $\frac{3}{5} π$ D、 $\frac{4}{5} π$

查看试题解析
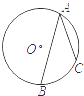4. 一元二次方程 $x (2 x - 1) = 0$ 根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
5. 如图，以O为圆心的两个同心圆中，大圆的弦AB切小圆于点C，若∠AOB=120°，则大圆半径R与小圆半径r之间满足（）

A、 $R = \sqrt{3} r$ B、R=3r C、R=2r D、 $R = 2 \sqrt{2} r$

查看试题解析
6. 若二次函数 $y = {ax}^{2} + bx + c$ 的x与y的部分对应值如下表，则当 $x = 1$ 时，y的值为 $($ 　　 $)$

x

$- 7$

$- 6$

$- 5$

$- 4$

$- 3$

$- 2$

y

$- 27$

$- 13$

$- 3$

3

5

3

A、5 B、 $- 3$ C、 $- 13$ D、 $- 27$

查看试题解析
7. 如图，⊙O的半径为1，点 O到直线 a的距离为2，点 P是直线a上的一个动点，PA切⊙O于点 A，则 PA的最小值是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\sqrt{5}$

查看试题解析
8. 某品牌服装原价173元，连续两次降价 $x \frac{0}{0}$ 后售价价为127元，下面所列方程中正确的是（）

A、 $173 {(1 + x %)}^{2} = 127$ B、 $173 (1 - 2 x %) = 127$ C、 $173 {(1 - x %)}^{2} = 127$ D、 $127 {(1 + x %)}^{2} = 173$

查看试题解析
9. 如图，直角三角板ABC的斜边AB=12㎝，∠A=30°，将三角板ABC绕C顺时针旋转90°至三角板 $A^{'} B^{'} C^{'}$ 的位置后，再沿CB方向向左平移，使点落在原三角板ABC的斜边AB上，则三角板平移的距离为（）

A、6㎝ B、4㎝ C、（6－ $2 \sqrt{3}$ ）㎝ D、（ $4 \sqrt{3} - 6$ ）㎝

查看试题解析
10. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，有以下结论：① $a b c > 0$ ；② $a + b + c < 0$ ；③ $a - b + c > 1$ ；④ $4 a - 2 b + c < 0$ ；⑤ $a + 1 < c$ ．其中正确结论的个数为（）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

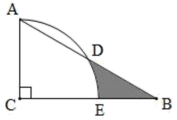
11. 从1，2，﹣3三个数中，随机抽取两个数相乘，积是正数的概率是．

查看试题解析
12. $y = - 2 x^{2} + 5 x - 1$ 的图象不经过象限；

查看试题解析
13. 关于x的一元二次方程 $x^{2} + (m - 2) x + m + 1 = 0$ 有两个相等的实数根，则m的值是．

查看试题解析
14. 在平面直角坐标系中有一个对称图形，点 A（3，2）与点 B（3，-2）是此图形上的互为对称点，则在此图形上的另一点 C（-1，-3）的对称点坐标为；

查看试题解析
15. 如图，在 Rt△ABC中，∠ACB=90°，∠ABC=30°，AC=6，以C为圆心，以AC的长为半径作弧，交AB于点D，交BC于点E，则图中阴影部分的面积是；（结果保留 $π$ ）

查看试题解析
16. 如图，已知 A、B 两点的坐标分别为（2，0）、（0，2），⊙C的圆心坐标为（-2，0），半径为2．若D是⊙C上的一个动点，线段DA与y轴交于点E，则△ABE面积的最小值是；

查看试题解析
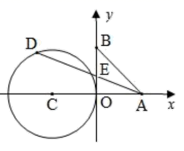17. 如图，直线 $y = \sqrt{3} x + \sqrt{3}$ 交x轴于点A，交y轴于点B．以A为圆心，以AB为半径作弧交x轴于点A₁；过点A₁作x轴的垂线，交直线 AB于点B₁ ，以A为圆心，以AB₁为半径作弧交x轴于点 A₂；…，如此作下去，则点 $A_{n}$ 的坐标为；

查看试题解析

三、解答题

18. 解下列方程：

(1)、 $(x + 1) (x - 2) = x + 1$

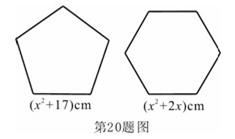
(2)、 $2 x^{2} + 5 x = 3$

查看试题解析
19. 如图，用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形，其中正五边形的边长为( $x^{2} + 17$ ) $c m$ ，正六边形的边长为( $x^{2} + 2 x$ )cm（其中 $x > 0$ )，求这两段铁丝的总长

查看试题解析
20. 一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同。

(1)、求摸出1个球是白球的概率；

(2)、摸出1个球，记下颜色后放回，并搅均，再摸出1个球。求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）；

(3)、现再将n个白球放入布袋，搅均后，使摸出1个球是白球的概率为 $\frac{5}{7}$ 。求n的值。

查看试题解析
21. 如图，已知 AB是⊙O的直径，点C在⊙O上，AD⊥DC于点 D，AC平分∠DAB．

(1)、求证：直线CD是⊙O的切线；

(2)、若 AB=4，∠DAB=60°，求AD的长．

查看试题解析
22. 阅读与理解：
图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．

(1)、操作与证明：
操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；

　

(2)、操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；

(3)、猜想与发现：
根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？

查看试题解析
23. 如图，已知二次函数 $y = - x^{2} + b x + 3$ 的图象与x轴的两个交点为A（4，0）与点C，与y轴交于点B．

(1)、求此二次函数关系式和点C的坐标；

(2)、请你直接写出△ABC的面积：

(3)、在x轴上是否存在点P，使得△PAB是等腰三角形？若存在，请你直接写出点P的坐标；若不存在，请说明理由．

查看试题解析

x	$- 7$	$- 6$	$- 5$	$- 4$	$- 3$	$- 2$
y	$- 27$	$- 13$	$- 3$	3	5	3