上海市闵行10校联考2020-2021学年八年级上学期数学期中试卷

试卷更新日期：2020-12-24 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列各式中，二次根式 $\sqrt{a - b}$ 的有理化因式是（）

A、 $\sqrt{a+b}$ B、 $\sqrt{a} + \sqrt{b}$ C、 $\sqrt{a - b}$ D、 $\sqrt{a} - \sqrt{b}$

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{a^{2} - b^{2}}$ B、 $\sqrt{27}$ C、 $\sqrt{a^{3} - a^{2} b}$ D、 $\sqrt{0.5 a}$

查看试题解析
3. 下列方程是关于x的一元二次方程的是（）

A、 $x^{2} - 2 x = \frac{1}{x}$ B、 $x (x - 2) = x^{2}$ C、 $x^{2} = 3 (x + 2)$ D、 $a x^{2} + b x + c = 0$

查看试题解析
4. 下列关于x的一元二次方程中，没有实数根的是（）

A、 $x^{2} - 6 x + 1 = 0$ B、 $2 x^{2} + 2 = x$ C、 $4 x^{2} + 4 x + 1 = 0$ D、 $4 x^{2} - (m - 1) x = 3$

查看试题解析
5. 下列命题是真命题的是（）

A、两个锐角的和还是锐角； B、全等三角形的对应边相等； C、同旁内角相等，两直线平行； D、等腰三角形既是轴对称图形，又是中心对称图形．

查看试题解析
6. 如图，在△ABC中，∠ACB＝90°，CH⊥AB，垂足为点H，AD平分∠BAC，与CH相交于点D，过点D作DE∥BC，与边AB相交于点E，那么下列结论中一定正确的是（）

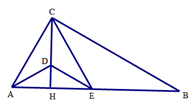A、DA=DE B、AC=EC C、AH＝EH D、CD＝ED

查看试题解析

二、填空题

7. 化简： $\sqrt{\frac{2}{3}}$ =

查看试题解析
8. 化简： $\sqrt{x^{3} y^{2}} (y \geq 0) =$ ．

查看试题解析
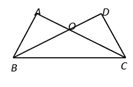
9. 已知： $\sqrt{a^{2} - 2 a + 1} = 1 - a$ ，那么a的取值范围是．

查看试题解析
10. 不等式 $\sqrt{2} x - 3 < \sqrt{3} x$ 的解集是.

查看试题解析
11. 已知最简二次根式 $x \sqrt{x + 5}$ 与 $3 \sqrt{3}$ 是同类二次根式，x= ．

查看试题解析
12. 方程 $\frac{1}{2} x^{2} = x$ 的根是．

查看试题解析
13. 在实数范围内分解因式： $2 x^{2} - 3 x - 1 ＝$ .

查看试题解析
14. 方程 $3 x^{2} + 4 x - 2 = 0$ 的根的判别式的值为．

查看试题解析
15. 某种商品原价800元，经过两次降价后售价为612元，其中二次降价的百分率比第一次降价的百分率多5%，如果设第一次降价的百分率为x，那么根据题意所列出的方程为（只列出方程，无需求解）．

查看试题解析
16. 把命题“同位角相等，两直线平行”改写成“如果……那么……”的形式是.

查看试题解析
17. 如图，已知 $A C = D B$ ，要使 $Δ B A C$ ≌ $Δ C D B$ 成立，还需填加一个条件，那么这个条件可以是．（只需写出一个即可）

查看试题解析
18. 如图，三角形纸片ABC中∠A＝75°，∠B＝72°，将三角形纸片的一角折叠，使点C落在△ABC内，如果∠1＝32°，那么∠2＝度．

查看试题解析

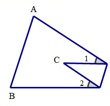
三、解答题

19. 如图，已知，AB⊥BD，AC⊥CD，且∠BAD＝∠CAD．
求证：AD⊥BC．

查看试题解析
20. 计算： $(\sqrt{0.5} + 2 \sqrt{\frac{1}{3}}) - (\sqrt{18} - \sqrt{27})$

查看试题解析
21. 解方程： $(x + 1) (x + 2) = 12$

查看试题解析
22. 用配方法解方程： $2 x^{2} + 6 x - 1 = 0$

查看试题解析
23. 先化简，再求值： $[\frac{4}{(\sqrt{x} + \sqrt{y}) (\sqrt{x} - \sqrt{y})} + \frac{\sqrt{x} + \sqrt{y}}{\sqrt{x y} (\sqrt{y} - \sqrt{x})}] \div \frac{\sqrt{x} - \sqrt{y}}{\sqrt{x y}}$ ，其中x＝1，y＝2．

查看试题解析
24. 已知关于x的一元二次方程 $(m + 1) x^{2} - 3 x + 2 = 0$ （m为常数）．

(1)、如果方程有两个不相等的实数根，求m的取值范围；

(2)、如果方程有两个相等的实数根，求m的取值；

(3)、如果方程没有实数根，求m的取值范围；

查看试题解析
25. 某工程队，在工地一边的靠墙处（墙的长度为70米），用120米长的铁栅栏围成一个所占地面为长方形的临时仓库，铁栅栏只围三边，并且在平行于墙的一边开一扇宽为2米的门，如果围成的长方形临时仓库的面积为1800平方米，求长方形的两条边长．

查看试题解析
26. 如图，已知，在 $△ A B C$ 中，点D是边AC的中点，点E是边BC的延长线上一点，过点A作BE的平行线与线段ED的延长线相交于点F，连结AE．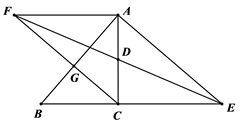

(1)、求证：AF＝CE．

(2)、连结CF，交边AB于点G，如果CF⊥AB，求证： $∠ A B C + ∠ A E B = 90 °$ ．

查看试题解析
27. 如图，已知， $△ A B C$ 是等边三角形，CE是 $△ A B C$ 的外角∠ACM的平分线，点D为射线BC上一点，且∠ADE＝∠ABC，DE与CE相交于点E．

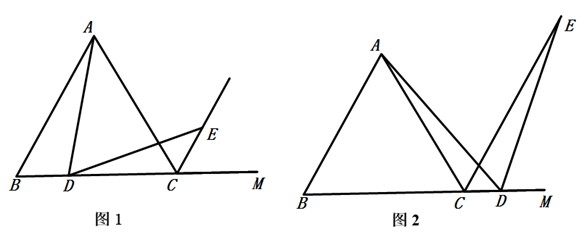(1)、如图1，如果点D在边BC上，求证：AD＝DE；

(2)、如图2，如果点D在边BC的延长线上，那么（1）中的结论“AD＝DE”还成立吗？请说明理由；

(3)、如果 $△ A B C$ 的边长为4，且∠DAC＝30°，请直接写出线段BD的长度．（无需写出解题过程）

查看试题解析