初中数学苏科版七年级上学期期末复习专题6 整式加减混合运算

试卷更新日期：2020-12-24 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列式子中计算正确的是（）

A、 $(- x + 3 y) - (2 x - 5 y) = - x - 2 y$ B、 $1 - 2 (x^{2} - x + 1) = - 2 x^{2} + 2 x - 1$ C、 $(2 x + y - z) - (5 x + y - z) = - 2 x - 4 y - 2 z$ D、 $2 (x^{2} - 2 x y + y^{2}) - (x^{2} - 4 x y + 2 y^{2}) = x^{2} + 4 y^{2}$

查看试题解析
2. 李老师做了个长方形教具，其中一边长为 $2 a + b$ ，相邻的一边长为 $a - b$ ，则该长方形周长为（）

A、 $3 a$ B、 $10 a - b$ C、 $6 a$ D、 $6 a + b$

查看试题解析
3. 一多项式与 $2 a^{2} + 3 a - 7$ 的和为 $a^{2} - 4 a + 9$ ，则这个多项式为（　）

A、 $- a^{2} - a + 2$ B、 $- a^{2} - 7 a + 16$ C、 $- a^{2} - a + 16$ D、 $3 a^{2} - a + 2$

查看试题解析
4. 如果 $M = x^{2} + 6 x + 22, N = - x^{2} + 6 x - 3$ ，那么 $M$ 与 $N$ 的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、无法确定

查看试题解析
5. 已知有理数a、b、c在数轴上的位置如图所示，则化简|a+b|﹣|b﹣c|的结果是（）

A、a+c B、c﹣a C、﹣a﹣c D、a+2b﹣c

查看试题解析
6. 若2＜x＜3，那么化简|2－x|－|x－3|结果是（）

A、－2x+5 B、2x－5 C、1 D、－5

查看试题解析
7. 若关于a，b的多项式3(a²﹣2ab﹣b²)﹣(a²+mab+2b²)不含ab项，则m的值是（）

A、4 B、0 C、﹣6 D、﹣8

查看试题解析
8. 定义：若 $a + b = n$ ，则称a与b是关于数n的“平衡数”. 比如3与-4是关于-1的“平衡数”，5与12是关于17的“平衡数”. 现有 $a = 3 x^{2} - 10 k x + 12$ 与 $b = - 3 x^{2} + 5 x - 2 k$ （k为常数）始终是关于数n的“平衡数”，则 $n =$ （）

A、11 B、12 C、13 D、14

查看试题解析
9. 如图，线段AB上有C，D两点，以AC，CD，BD为直径的圆的周长分别是 $C_{1}$ 、 $C_{2}$ 、 $C_{3}$ ，以AB为直径的圆的周长为C，下列结论正确的是（）

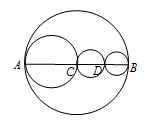A、 $C_{1}$ ＋ $C_{2}$ ＝C＋ $C_{3}$ B、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＝C C、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＞C D、 $C_{1}$ ＋ $C_{2}$ ＋ $C_{3}$ ＜C

查看试题解析
10. 如图1是长为 $a$ ，宽为 $b$ 的小长方形卡片，把六张这样的小长方形卡片不重叠地放在一个底面为长方形（长为4，宽为3）的盒子底部（如图2），盒子底部未被卡片覆盖的部分用阴影表示，则两块阴影部分的周长之和为（）

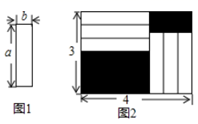A、8 B、10 C、12 D、14

查看试题解析

二、填空题

11. 已知单项式2a^mb²与﹣ $\frac{1}{2}$ a⁴bⁿ^﹣¹的差是单项式，那么m²﹣n=.

查看试题解析
12. 若x+y=3，xy=2，则（5x+2）﹣（3xy﹣5y）=

查看试题解析
13. 已知A＝2x²+3xy+2x﹣1，B＝4x²+xy+3x﹣2.当y＝时，代数式2A﹣B的值与x无关.

查看试题解析
14. 关于 $x$ 的多项式 $5 x^{3} - 6 x^{2} + 2 x - 3$ 与 $2 x^{3} + 3 m x^{2} - x + 2$ 的和不含二次项，则m= ．

查看试题解析
15. 对于任意实数a，b，定义关于“ 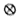”的一种运算如下：a 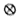b=2a+b，例如3 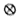4=2×3+4=10．若x 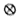(-y)=2，且y 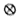(-x)=5，则x+y的值为。

查看试题解析
16. 小明同学在做一道题:“已知两个多项式 A,B,计算 2A+B,误将“2A+B”看成“A+2B”,求得的结果为9x $^{2}$ + 2x - 6 .已知 A+B= 2x $^{2}$ - 4x + 9 ,则 2A+B的正确答案为.

查看试题解析
17. 当 $1 < x < 3$ 时，化简 $\frac{| x - 3 | + | x - 1 |}{x - 2}$ 的结果是.

查看试题解析
18. 如图是一个长方形的储物柜，它被分成大小不同的正方形①②③④和一个长方形⑤.若要计算长方形⑤的周长，则只需要知道哪个小正方形的周长？你的选择是正方形（填编号）.

查看试题解析

三、解答题

19. 有理数a、b、c在数轴上的位置如图．化简： $| a - b | + | b - c | + | c - a |$ ．

查看试题解析
20. 化简：

(1)、 $- 3 x^{2} y + 2 x^{2} y + 3 x y^{2} - 2 x y^{2}$ ；　　

(2)、 $5 (a + b) - 4 (3 a - 2 b) + 3 (2 a - 3 b)$

查看试题解析
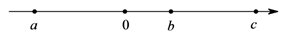21. 已知关于x，y的多项式 $3 x^{3} + m y - 8$ 与 $- n x^{3} + 2 y + 7$ 的差中，不含有x，y的项，求 $n^{m} + m n$ 的值.

查看试题解析
22. 七年级某同学做习题：已知两个多项式A，B，A＝x²+2x﹣1，计算-2A+B.他误将-2A+B写成了2A+B，结果得到答案x²+5x﹣6，请你帮助他求出正确的答案.

查看试题解析
23. 试说明把一个两位数的十位上的数字与个位上的数字互换位置后，所得的新两位数与原两位数的和能被11整除

查看试题解析
24. 数学课上李老师让同学们做一道整式的化简求值题，李老师把整式 $(7 a^{3} - 6 a^{3} b) - 3 (- a^{3} - 2 a^{3} b +$ $\frac{10}{3} a^{3} - 1)$ 在黑板上写完后，让一位同学随便给出一组 $a$ ， $b$ 的值，老师说答案．当刘阳刚说出 $a$ ， $b$ 的值时，李老师不假思索，立刻说出了答案．同学们莫名其妙，觉得不可思议，但李老师用坚定的口吻说：“这个答案准确无误”．你能说出其中的道理吗？

查看试题解析
25. 材料：若一个正整数，它的各个数位上的数字是左右对称的，则称这个正整数是对称数.例如：正整数22是两位对称数；正整数797是三位对称数；正整数4664是四位对称数；正整数12321是五位对称数.
根据材料，完成下列问题：

(1)、最大的两位对称数与最小的三位对称数的和为

(2)、若将任意一个四位对称数拆分为前两位数字顺次表示的两位数和后两位数字顺次表示的两位数，则这两个两位数的差一定能被9整除吗？请说明理由.

(3)、如果一个四位对称数的个位数字与十位数字的和等于10，并且这个四位对称数能被7整除，请求出满足条件的四位对称数.

查看试题解析
26. 已知，7张如图1的长为a，宽为b（其中a＞b）的小长方形纸片，按图2方式不重叠地放在长方形ABCD内，长方形ABCD的长AD=m，未被覆盖的部分的长方形MNPD的面积记作S₁ ，长方形BEFG的面积记作S₂.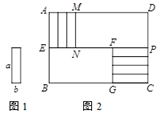

(1)、当 $a = 5$ ， $b = 1$ ， $m = 14$ 时，求S₁ $-$ S₂的值；

(2)、①请用含有a、b、m的代数式表示S₁ $-$ S₂；
②若S₁ $-$ S₂的值与m的取值无关，求a，b满足的数量关系.

查看试题解析