初中数学苏科版八年级上学期期末复习专题（11）一次函数与二元一次方程

试卷更新日期：2020-12-24 类型：复习试卷

进入出卷网下载

一、单选题

1. 直线y=x+1与y=–2x–4交点在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知函数 $y = x - 3$ ， $y = - \frac{1}{3} x + 1$ ， $y = k x + 6$ 的图象交于一点，则 $k$ 值为（）．

A、 $2$ B、 $- 2$ C、 $3$ D、 $- 3$

查看试题解析
3. 已知二元一次方程组 ${\begin{matrix} x - y = - 5 \\ x + 2 y = - 2 \end{matrix}$ 的解为 ${\begin{matrix} x = - 4 \\ y = 1 \end{matrix}$ ，则在同一平面直角坐标系中，直线 $l_{1} : y = x + 5$ 与直线 $l_{2} : y = - \frac{1}{2} x - 1$ 的交点坐标为（）

A、 $(1, - 4)$ B、 $(- 4, 1)$ C、 $(4, 1)$ D、 $(1, 4)$

查看试题解析
4. 若方程组 ${\begin{matrix} - m x + y = n \\ e x + y = f \end{matrix}$ 的解为 ${\begin{matrix} x = 4 \\ y = 6 \end{matrix}$ ，则直线y=mx+n与y=﹣ex+f的交点坐标为（）

A、（﹣4，6） B、（4，6） C、（4，﹣6） D、（﹣4，﹣6）

查看试题解析
5. 小亮在同一直角坐标系内作出了 $y = - 2 x + 2$ 和 $y = - \frac{1}{2} x - 1$ 的图象，方程组 ${\begin{array}{l} 2 x + y = 2 \\ \frac{1}{2} x + y = - 1 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ B、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = 2 \end{array}$ D、 ${\begin{array}{l} x = - 2 \\ y = - 2 \end{array}$

查看试题解析
6. 已知函数y=k₁x+b₁与函数y=k₂x+b₂的图象如图所示，则方程组 ${\begin{matrix} k_{1} x + b_{1} - y = 0 \\ k_{2} x + b_{2} - y = 0 \end{matrix}$ 的解为（）

A、 ${\begin{matrix} x = - 1 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = - 1 \\ y = 5 \end{matrix}$ C、 ${\begin{matrix} x = 5 \\ y = 5 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = 4 \end{matrix}$

查看试题解析
7. 已知直线y＝－x＋4与y＝x＋2如图所示，则方程组 ${\begin{array}{l} y = - x + 4 \\ y = x + 2 \end{array}$ 的解为（）

A、 ${\begin{array}{l} x = 3 \\ y = 1 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 3 \end{array}$ C、 ${\begin{array}{l} x = 0 \\ y = 4 \end{array}$ D、 ${\begin{array}{l} x = 4 \\ y = 0 \end{array}$

查看试题解析
8. 如图，以两条直线l₁ ， l₂的交点坐标为解的方程组是（）

A、 B、 C、 D、

查看试题解析
9.
如图一次函数y₁=ax+b和y₂=cx+d在同一坐标系内的图象，则 $\{\begin{matrix} y = a x + b \\ y = c x + d \end{matrix}$ 的解 $\{\begin{matrix} x = m \\ y = n \end{matrix}$ 中（　　）

A、m＞0，n＞0 B、m＞0，n＜0 C、m＜0，n＞0 D、m＜0，n＜0

查看试题解析
10. 已知直线 $l_{1} ： y = k x + b (k > 0)$ 过点 $(- \sqrt{3} ， 0)$ 且与x轴相交夹角为30度，P为直线 $l$ 上一动点， $A (\sqrt{3} ， 0) ， B (3 \sqrt{3} ， 0)$ 为x轴上两点，当 $P A + P B$ 时取到最小值时，P的坐标为（）

A、 $(\sqrt{3} ， 2)$ B、 $(1 ， \sqrt{3})$ C、 $(\sqrt{3} ， 3)$ D、 $(2 ， \sqrt{3})$

查看试题解析

二、填空题

11. 已知直线y=x-3与y=2x+2的交点为（-5，-8），则方程组 ${\begin{array}{l} y = x - 3 \\ y = 2 x + 2 \end{array}$ 的解是．

查看试题解析
12. 如图，直线 $y = k x + b$ 与 $y = m x + n$ 相交于点M ，则关于x ， y的方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解是．

查看试题解析
13. 如图，已知一次函数y=kx-b与y= $\frac{1}{3}$ x的图像相交于点A(a，1)，则关于x的方程 $(k - \frac{1}{3}) x$ $= b$ 的解x=.

查看试题解析
14. 如图，已知直线y＝ax+b和直线y＝kx交于点P，则关于x，y的二元一次方程组 ${\begin{array}{l} y = k x \\ y = a x + b \end{array}$ 的解是．

查看试题解析
15. 直线 y=2x 与直线 y=-x+b 的交点坐标是(a，4)则关于 x，y 为方程组 ${\begin{matrix} y = 2 x \\ y = - x + b \end{matrix}$ 的解是

查看试题解析
16. 在同一平面直角坐标系中，若直线 $y = 3 x - 1$ 与直线 $y = x - k$ 的交点在第四象限的角平分线上，则 $k$ 的值为.

查看试题解析
17. 若二元一次方程组 ${\begin{array}{l} 4 x - y = 1 ， \\ y = 2 x - m \end{array}$ 的解是 ${\begin{array}{l} x = 2 ， \\ y = 7 ， \end{array}$ 则一次函数 $y = 2 x - m$ 的图象与一次函数 $y = 4 x - 1$ 的图象的交点坐标为．

查看试题解析
18. 如图，直线 $y = k x$ 和直线 $y = a x + b$ 相交于点M，若关于 $x ， y$ 的方程组 ${\begin{array}{l} y = k x \\ y = a x + b \end{array}$ 的解是 $x ， y$ ，那么 $x + y$ = ．

查看试题解析

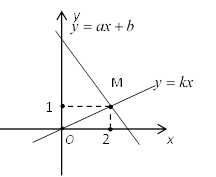
三、综合题

19. 若正比例函数y=﹣x的图象与一次函数y=x+m的图象交于点A，且点A的横坐标为﹣1．
（1）求该一次函数的解析式；
（2）直接写出方程组 $\{\begin{matrix} y = - x \\ y = x + m \end{matrix}$ 的解．

查看试题解析
20. 如图，在平面直角坐标系中，直线y=−2x+12与x轴交于点A，与y轴交于点B，与直线y=x交于点C．

(1)、求点C的坐标．

(2)、若P是x轴上的一个动点，直接写出当△POC是等腰三角形时P的坐标．

(3)、在直线AB上是否存在点M，使得△MOC的面积是△AOC面积的2倍？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析
21. （1）求一次函y=2x﹣2的图象l₁与y= $\frac{1}{2}$ x﹣1的图象l₂的交点P的坐标．
（2）求直线l₁与y轴交点A的坐标；求直线l₂与x轴的交点B的坐标；
（3）求由三点P、A、B围成的三角形的面积．

查看试题解析
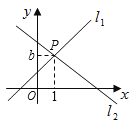
22.
如图，直线l₁：y＝x+1与直线l₂：y＝mx+n相交于点P（1，b）．①求b的值；②不解关于x ， y的方程组 $\{\begin{matrix} y = x + 1 \\ y = m x + n \end{matrix}$ ，请你直接写出它的解；
③直线l₃：y=nx+m是否也经过点P？请说明理由．

查看试题解析
23. 如图，在平面直角坐标系中AD⊥BC，垂足为D，交y轴于点H，直线BC的解析式为y=-2x+4.点H(0，2)，

(1)、求证：△AOH≌△COB；

(2)、求D点的坐标.

查看试题解析
24. 如图，直线y=-x+1和直线y=x-2相交于点P，分别与y轴交于A、B两点．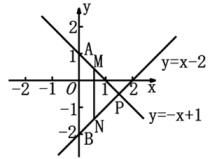

(1)、求点P的坐标；

(2)、求△ABP的面积；

(3)、M、N分别是直线y=-x+1和y=x-2上的两个动点，且MN∥y轴，若MN=5，直接写出M、N两点的坐标．

查看试题解析
25. 如图，在平面直角坐标系xOy中，已知正比例函数 $y = \frac{3}{4} x$ 与一次函数 $y = - x + 7$ 的图象交于点A．

(1)、求点A的坐标；

(2)、设x轴上有一点P（a，0），过点P作x轴的垂线（垂线位于点A的右侧），分别交 $y = \frac{3}{4} x$ 和 $y = - x + 7$ 的图象于点B、C，连接OC．若BC= $\frac{7}{5}$ OA，求△OBC的面积．

查看试题解析
26. 如图，已知y=3x+3与x轴交于点B，与y轴交于点A，与函数y=x的图象交于点P

(1)、在该坐标系中画出函数y= $\frac{1}{3}$ $x- 1$ 的图象，并说明点P也在函数y= $\frac{1}{3}$ $- 1$ 的图象上；

(2)、设直线y= $\frac{1}{3} x- 1$ 与x轴交于点C，与y轴交于点D，求证：PO平分∠APC；

(3)、连接AC，求△APC的面积；

(4)、在y轴上，是否存在点M，使△ACM为等腰三角形?若存在，请直接写出符合条件的所有点M的坐标；若不存在，请说明理由。

查看试题解析

初中数学苏科版八年级上学期期末复习专题（11） 一次函数与二元一次方程

一、单选题

二、填空题

三、综合题

初中数学苏科版八年级上学期期末复习专题（11）一次函数与二元一次方程