新疆维吾尔自治区伊犁哈萨克自治州2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-12-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中是轴对称图形的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 分式 $\frac{1}{x - 1}$ 有意义，则x的取值范围是（）

A、 $x > 1$ B、 $x \neq 1$ C、 $x < 1$ D、一切实数

查看试题解析
3. 下列计算中，正确的是（　　）

A、x³•x²=x⁴ B、x（x-2）=-2x+x² C、（x+y）（x-y）=x²+y² D、3x³y²÷xy²=3x⁴

查看试题解析
4. 在 $\frac{1}{x}$ ， $\frac{a b^{2}}{5}$ ， $- 0.7 x y + y^{3}$ ， $\frac{m + n}{m}$ ， $\frac{b - c}{5 + a}$ ， $\frac{3 x^{2}}{π}$ 中，分式有（）

A、2个； B、3个； C、4个； D、5个；

查看试题解析
5. 已知△ABC的周长是24，且AB=AC，又AD⊥BC，D为垂足，若△ABD的周长是20，则AD的长为（）

A、6 B、8 C、10 D、12

查看试题解析
6. 如图所示，OP平分 $∠ A O B$ ， $P A ⊥ O A$ ， $P B ⊥ O B$ ，垂足分别为A、B ．下列结论中不一定成立的是（）．

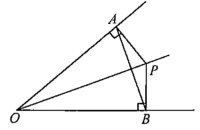A、 $P A = P B$ B、PO平分 $∠ A P B$ C、 $O A = O B$ D、AB垂直平分OP

查看试题解析
7. 如图，△ABC中，∠C=90°，AD平分∠BAC ， BC=10，BD=6，则点D到AB的距离是（　　）

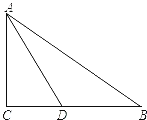A、4 B、5 C、6 D、7

查看试题解析
8. 已知x^m＝6，xⁿ＝3，则x^2m^―ⁿ的值为（）

A、9 B、 $\frac{3}{4}$ C、12 D、 $\frac{4}{3}$

查看试题解析
9. 若（a﹣3）²+|b﹣6|＝0，则以a、b为边长的等腰三角形的周长为（）

A、12 B、15 C、12或15 D、18

查看试题解析
10. 如图，C为线段AE上一动点（不与A、E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连结PQ，以下五个结论：①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP；⑤∠AOB=60°其中完全正确的是（）

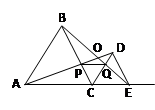A、①②③④ B、②③④⑤ C、①③④⑤ D、①②③⑤

查看试题解析

二、填空题

11. 等腰三角形的一个外角是140° ，则其底角是

查看试题解析
12. 计算：-4(a²b^-1)²÷8ab²= ．

查看试题解析
13. 若分式 $\frac{x - 2}{2 x + 1}$ 的值为零，则x的值等于．

查看试题解析
14. 已知a+b=3，ab=2，则a²b+ab²= ．

查看试题解析
15. 已知点 P（1﹣a，a+2）关于 y 轴的对称点在第二象限，则 a 的取值范围是.

查看试题解析
16. 如图，在△ABC 中，AB＝AC，AB 的垂直平分线 MN 交 AC 于 D 点．若 BD 平分∠ABC，则∠A＝°．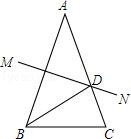

查看试题解析
17. 如图，已知△ABC的周长是22，OB、OC分别平分∠ABC和∠ACB ， OD⊥BC于D ，且OD=3，△ABC的面积是．

查看试题解析
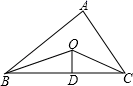18. 如图，已知∠1=∠2，请你添加一个条件，使得△ABD≌△ACD．（添一个即可）

查看试题解析
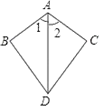19. 多项式4x²+1加上一个单项式，使它成为一个整式的完全平方，则这个单项式可以是 .（填写符合条件的一个即可）

查看试题解析
20. 对于实数a，b，c，d，规定一种运算 $| \begin{matrix} a b \\ c d \end{matrix} |$ =ad-bc，如 $| \begin{array}{r} 1 & 0 \\ 2 & (- 2) \end{array} |$ =1×(-2)-0×2=-2，那么当 $| \begin{array}{l} (x + 1) & (x + 2) \\ (x - 3) & (x - 1) \end{array} |$ =27时，则x=.

查看试题解析

三、解答题

21. 因式分解:

(1)、4x²-9

(2)、-3x²+6xy-3y²

查看试题解析
22. 解下列方程并检验

(1)、 $\frac{2 x}{x + 3} + 1 = \frac{7}{2 x + 6}$

(2)、 $\frac{3}{2 x - 2} + \frac{1}{1 - x} = 3$

查看试题解析
23. 先化简，再求值：[(x-2y)²-x(x-4y)-8xy]÷4y，其中x=-1，y=2.

查看试题解析
24. 先化简 $(\frac{a + 1}{a - 1} + \frac{1}{a^{2} - 2 a + 1}) \div \frac{a}{a - 1}$ ，再从0，1，2中选一个合适的值代入求值.

查看试题解析
25. 如图所示，已知在△ABC中，AB=AC，BD和CE分别是∠ABC和∠ACB的角平分线，且BD和CE相交于O点.

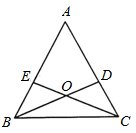(1)、试说明△OBC是等腰三角形；

(2)、连接OA，试判断直线OA与线段BC的关系，并说明理由.

查看试题解析
26. 某商店第一次用3000元购进某款书包，很快卖完，第二次又用2400元购进该款书包，但这次每个书包的进价是第一次进价的1.2倍，数量比第一次少了20个.

(1)、求第一次每个书包的进价是多少元?

(2)、若第二次进货后按80元/个的价格销售，恰好销售完一半时，根据市场情况，商店决定对剩余的书包按同一标准一次性打折销售，但要求这次的利润不少于480元，问最低可打几折？

查看试题解析
27. 八（1）班同学到野外上数学活动课，为测量池塘两端A、B的距离，设计了如下方案：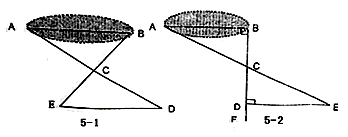

（Ⅰ）如图5-1，先在平地上取一个可直接到达A、B的点C，连接AC、BC，并分别延长AC至D，BC至E，使DC=AC，EC=BC，最后测出DE的距离即为AB的长；

（Ⅱ）如图5-2，先过B点作AB的垂线BF，再在BF上取C、D两点使BC=CD，接着过D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离.

阅读后1回答下列问题：

(1)、方案（Ⅰ）是否可行？说明理由.

(2)、方案（Ⅱ）是否可行？说明理由.

(3)、方案（Ⅱ）中作BF⊥AB，ED⊥BF的目的是；若仅满足∠ABD=∠BDE≠90°，方案（Ⅱ）是否成立？.

查看试题解析