新疆维吾尔自治区乌鲁木齐市2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-23 类型:期末考试
一、单选题
-
1. 下列图形具有两条对称轴的是( )A、等边三角形 B、平行四边形 C、矩形 D、正方形2. 在下列长度的三条线段中,不能组成三角形的是( )A、2 cm, 3 cm. 4cm B、3 cm, 6 cm. 6cm C、2 cm, 2 cm, 6cm D、5 cm, 6 cm. 7 cm3. 下列计算正确的是( )A、 B、 C、 D、4. 已知一个多边形的内角和是 ,则该多边形的边数为( )A、4 B、6 C、8 D、105. 为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条,这样做的道理是( )
 A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等6. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A、两点之间,线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行,内错角相等6. 如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )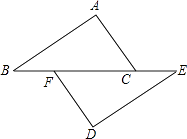 A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC7. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =58. 如图,在 中, , ,以点 为圆心,小于 的长为半径作弧,分别交 , 于 两点;再分别以点 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 .若 的面积为9,则 的面积为( )
A、AB=DE B、AC=DF C、∠A=∠D D、BF=EC7. 某工厂计划生产300个零件,由于采用新技术,实际每天生产零件的数量是原计划的2倍,因此提前5天完成任务.设原计划每天生产零件x个,根据题意,所列方程正确的是( )A、 ﹣ =5 B、 ﹣ =5 C、 ﹣ =5 D、 ﹣ =58. 如图,在 中, , ,以点 为圆心,小于 的长为半径作弧,分别交 , 于 两点;再分别以点 为圆心,大于 长为半径作弧,两弧交于点 ,作射线 交 于点 .若 的面积为9,则 的面积为( ) A、3 B、 C、6 D、
A、3 B、 C、6 D、二、填空题
-
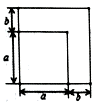
9. 将0.0021用科学记数法表示为.10. 若分式 有意义,x 的取值范围是.11. 分解因式: =.12. 计算: .13. 如图,两个四边形均为正方形,根据图形的面积关系,写出一个正确的等式.
 14. 如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 , 边于 , 点.若点 为 边的中点,点 为线段 上以动点,则 周长的最小值为
14. 如图,等腰三角形 的底边 长为 ,面积是 ,腰 的垂直平分线 分别交 , 边于 , 点.若点 为 边的中点,点 为线段 上以动点,则 周长的最小值为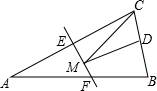
三、解答题
-
15. 计算:(1)、 ;(2)、 .16. 先化简,再求值: ,其中 .17. 在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形, 的顶点均在格点上,点 的坐标是 .
 (1)、将 沿 轴正方向平移3个单位得到 ,画出 ,并写出点 坐标;(2)、画出 关于 轴对称的 ,并写出点 的坐标.18. 如图,在 中, 与 的角平分线交于点 , .求 的度数.
(1)、将 沿 轴正方向平移3个单位得到 ,画出 ,并写出点 坐标;(2)、画出 关于 轴对称的 ,并写出点 的坐标.18. 如图,在 中, 与 的角平分线交于点 , .求 的度数.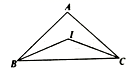 19. 如图, , ,求证: .
19. 如图, , ,求证: . 20. 已知:如图, 中, ,中线 和 交于点 .
20. 已知:如图, 中, ,中线 和 交于点 . (1)、求证: 是等腰三角形;21. 一辆汽车开往距离出发地 的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后速度提高 匀速行驶,并比原计划提前 到达目的地,求前一小时的行驶速度.22. (问题)
(1)、求证: 是等腰三角形;21. 一辆汽车开往距离出发地 的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后速度提高 匀速行驶,并比原计划提前 到达目的地,求前一小时的行驶速度.22. (问题)在 中, , ,点 在直线 上( 除外),分别经过点 和点 作 和 的垂线,两条垂线交于点 ,研究 和 的数量关系.
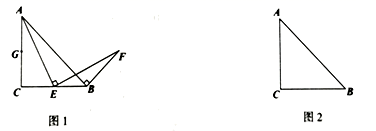 (1)、(探究发现)
(1)、(探究发现)某数学兴趣小组在探究 , 的关系时,运用“从特殊到一般”的数学思想,他们发现当点 是 中点时,只需要取 边的中点 (如图1),通过推理证明就可以得到 和 的数量关系,请你按照这种思路直接写出 和 的数量关系;
(2)、(数学思考)那么点 在直线 上( 除外)(其他条件不变),上面得到的结论是否仍然成立呢?
请你从“点 在线段 上”“点 在线段 的延长线上”“点 在线段 的反向延长线上”三种情况中,任选一种情况,在图2中画出图形,并证明你的结论.