宁夏银川十五中2019-2020学年八年级上学期数学期末考试试卷

试卷更新日期：2020-12-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数： $- 0.333 \dots, \sqrt{4}, 2.4, \sqrt{5}, - π, {(\sqrt{\frac{2}{3}})}^{2}, 6.0123456 \dots$ （小数部分由相继的自然数组成）.其中属于无理数的有（）

A、3个 B、4个 C、5个 D、6个

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{{(- 9)}^{2}}$ ＝－9 B、 $\sqrt{25}$ ＝±5 C、 $\sqrt[3]{{(- 1)}^{3}}$ ＝－1 D、(－ $\sqrt{2}$ )²＝4

查看试题解析
3. 已知点 $P (- 3, 5)$ ，则点 $P$ 到 $y$ 轴的距离是（）

A、5 B、3 C、4 D、-3

查看试题解析
4. 对于一次函数y=﹣2x+4，下列结论错误的是（　　）
　

A、函数值随自变量的增大而减小 B、函数的图象不经过第三象限 C、函数的图象向下平移4个单位长度得y=﹣2x的图象 D、函数的图象与x轴的交点坐标是（0，4）

查看试题解析
5. 某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图，则这组数据的众数和中位数分别是（）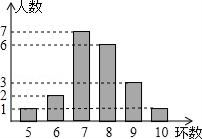

A、7，7 B、8，7.5 C、7，7.5 D、8，6.5

查看试题解析
6. 如图，已知 $∠ A = 45 ° ， ∠ B = 60 ° ， ∠ D = 25 °$ ，则 $∠ A E D =$ （）

A、 $105 °$ B、 $85 °$ C、 $120 °$ D、 $130 °$

查看试题解析
7. 已知方程组 ${\begin{matrix} m x + y = 0 \\ x + n y = 3 \end{matrix}$ 的解是 ${\begin{matrix} x = 1 \\ y = - 2 \end{matrix}$ ，则 $2 m + n$ 的值为（）

A、1 B、2 C、3 D、0

查看试题解析
8. 折叠长方形 $A B C D$ 的一边 $A D$ ，使点 $D$ 落在边 $B C$ 的点 $F$ 处，若 $A B = 8 c m ， B C = 10 c m$ ，求 $E C$ 的长为（）

A、3 B、4 C、 $\sqrt{3}$ D、5

查看试题解析

二、填空题

9. $\sqrt{16}$ 的平方根是．

查看试题解析
10. 在三角形ABC中，∠C=90°，AB=7，BC=5，则AC的长为.

查看试题解析
11. 面试时，某人的基本知识、表达能力、工作态度的得分分别是80分、70分、85分，若依次按30%、30%、40%的比例确定成绩，则这个人的面试成绩是.

查看试题解析
12. 已知一次函数 $y = 2 x + b$ 的图象经过点 $A (2, y_{1})$ 和 $B (- 1, y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“ $>$ ”、“ $<$ ”或“ $=$ ”）.

查看试题解析
13. 将“对顶角相等”改写为“如果...那么...”的形式，可写为.

查看试题解析
14. 若函数y=（m﹣1）x^|m|是正比例函数，则该函数的图象经过第象限．

查看试题解析
15. 已知 $y = a x + b$ 和 $y = k x$ 的图象交于点 $P (2, - 1)$ ，那么关于 $x, y$ 的二元一次方程组 ${\begin{matrix} a x - y + b = 0 \\ k x - y = 0 \end{matrix}$ 的解是.

查看试题解析
16. 如图，一个质点在第一象限及 $x$ 轴、 $y$ 轴上运动，第1次它从原点 $(0 ， 0)$ 运动到 $(0 ， 1)$ ，然后接着按图中箭头所示方向运动，即 $(0 ， 0) \to (0 ， 1) \to (1 ， 1) \to (1 ， 0) \to \dots$ ，那么第80次移动后质点所在位置的坐标是.

查看试题解析

三、解答题

17. 化简：

(1)、 $(3 + \sqrt{7}) (3 - \sqrt{7}) + \sqrt{2} (2 - \sqrt{2})$

(2)、 $3 \sqrt{12} - 3 \sqrt{\frac{1}{3}} + \sqrt{27}$

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} x + y = 4 \\ 2 x - y = - 1 \end{array}$

(2)、 ${\begin{array}{l} \frac{x}{3} - \frac{y}{4} = 1 \\ 3 x - 4 y = 2 \end{array}$ ．

查看试题解析
19. 已知，点 $A (0 ， 1) ， B (2 ， 0) ， C (4 ， 3)$ .

(1)、求 $Δ A B C$ 的面积；

(2)、画出 $Δ A B C$ 关于 $x$ 轴的对称图形 $Δ A_{1} B_{1} C_{1}$ .

查看试题解析
20. 如图，EF∥BC，AC平分∠BAF，∠B=80°.求∠C的度数.

查看试题解析
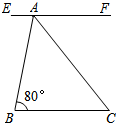21. 如图，△ABC中，D是BC上的一点．若AB＝10，BD＝6，AD＝8，AC＝17，求△ABC的面积．

查看试题解析
22. 为参加学校艺术节闭幕演出，八年级一班欲租用男、女演出服装若干套以供演出时使用，已知4套男装和6套女装租用一天共需租金490元，6套男装和10套女装租用一天共需790元.

(1)、租用男装、女装一天的价格分别是多少？

(2)、由于演出时间错开租用高峰时段，男装、女装一天的租金分别给予9折和8折优惠，若该班演出团由5名男生和12名女生组成，求在演出当天该班租用服装实际支付的租金是多少？

查看试题解析
23. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8

(1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；

(2)、分别计算甲、乙六次测试成绩的方差；

(3)、根据（1）、（2）计算的结果，你认为推荐谁参加全国比赛更合适，请说明理由．
（计算方差的公式：s²= $\frac{1}{n}$ [ ${(x_{1} - \bar{x})}^{2} + {(x_{2} - \bar{x})}^{2} + \dots + {(x_{n} - \bar{x})}^{2}$ ]）

查看试题解析
24. 某城市居民用水实行阶梯收费，每户每月用水量如果未超过20吨，按每吨1.9元收费.如果超过20吨，未超过的部分按每吨1.9元收费，超过的部分按每吨2.8元收费.设某户每月用水量为x吨，应收水费为y元.

(1)、分别写出每月用水量未超过20吨和超过20吨，y与x间的函数关系式.

(2)、若该城市某户5月份水费平均为每吨2.2元，求该户5月份用水多少吨.

查看试题解析
25. 如图，在 $Δ A B C$ 中，点 $D ， E ， F$ 分别在边 $A B ， A C ， B C$ 上，连接 $D E ， D F ， G$ 是 $D F$ 上一点，连接 $E G$ ，已知 $∠ 1 + ∠ 2 = 180 ° ， ∠ B = ∠ 3$ .

(1)、求证： $E G / / A B$ ；

(2)、求证： $∠ C = ∠ A E D$ .

查看试题解析
26. 如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2），动点N沿路线O→A→C运动.

(1)、求直线AB的解析式.

(2)、求△OAC的面积.

(3)、当△ONC的面积是△OAC面积的 $\frac{1}{4}$ 时，求出这时点N的坐标.

查看试题解析

	第一次	第二次	第三次	第四次	第五次	第六次
甲	10	8	9	8	10	9
乙	10	7	10	10	9	8