宁夏石嘴山市平罗县2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期:2020-12-23 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知△ABC中,AB=8,BC=5,那么边AC的长可能是下列哪个数( )A、15 B、12 C、3 D、23. 点 关于 轴的对称点 的坐标是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,把一个含30°角的直角三角尺的直角顶点放在直尺的一边上,如果∠1=20°,那么∠2的度数为( )
2. 已知△ABC中,AB=8,BC=5,那么边AC的长可能是下列哪个数( )A、15 B、12 C、3 D、23. 点 关于 轴的对称点 的坐标是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,把一个含30°角的直角三角尺的直角顶点放在直尺的一边上,如果∠1=20°,那么∠2的度数为( )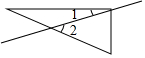 A、 B、 C、 D、6. 在 , , , , 中分式的个数有( )A、1个 B、2个 C、3个 D、4个7. 不能使两个直角三角形全等的条件是( ).A、一条直角边及其对角对应相等 B、斜边和两条直角边对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等8. 一只船顺流航行90千米与逆流航行60千米所用的时间相等,若水流的速度是2千米/时,求船在静水中的速度.如果设船在静水中的速度为x千米/时,可列出的方程是( )A、 B、 C、 D、
A、 B、 C、 D、6. 在 , , , , 中分式的个数有( )A、1个 B、2个 C、3个 D、4个7. 不能使两个直角三角形全等的条件是( ).A、一条直角边及其对角对应相等 B、斜边和两条直角边对应相等 C、斜边和一条直角边对应相等 D、两个锐角对应相等8. 一只船顺流航行90千米与逆流航行60千米所用的时间相等,若水流的速度是2千米/时,求船在静水中的速度.如果设船在静水中的速度为x千米/时,可列出的方程是( )A、 B、 C、 D、二、填空题
-
9. 计算: ;10. 使分式 有意义的 满足的条件是.11. 一个多边形的每个外角都是36°,这个多边形是边形12. 若 , ,则 =.13. 如果 是一个完全平方式,那么k的值是.14. 用直尺和圆规作一个角等于已知角的示意图如下,则要说明 ,需要说明 ,则这两个三角形全等的依据是.(写出全等的简写)
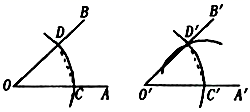 15. 如图,点B在点A的南偏西 方向,点C在点A的南偏东 方向,则 的度数为.
15. 如图,点B在点A的南偏西 方向,点C在点A的南偏东 方向,则 的度数为.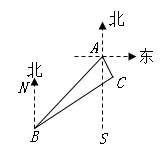 16. 如图,在 中, , 垂直平分 ,垂足为 ,交 于 ,若 的周长为 ,则 的长为
16. 如图,在 中, , 垂直平分 ,垂足为 ,交 于 ,若 的周长为 ,则 的长为
三、解答题
-
17. 利用乘法公式计算 :18. 因式分解:19. 解分式方程:20. 先化简,再求值:
,其中
21. 已知:如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=28°,求∠DAE的度数.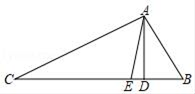 22. 按要求用尺规作图(要求:不写作法,但要保留作图痕迹.)
22. 按要求用尺规作图(要求:不写作法,但要保留作图痕迹.)已知: ,求作: 的角平分线 .
 23. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(3,1),C(2,3).
23. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,1),B(3,1),C(2,3). (1)、作出 关于 轴对称的图形 ,并写出 点的坐标;(2)、求 的面积.24. 如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC交AC于点D,过点D作DE⊥AB交AB于点E,过C作CF∥BD交ED于F.
(1)、作出 关于 轴对称的图形 ,并写出 点的坐标;(2)、求 的面积.24. 如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC交AC于点D,过点D作DE⊥AB交AB于点E,过C作CF∥BD交ED于F. (1)、求证:△BED≌△BCD;(2)、若∠A=36°,求∠CFD的度数.25. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?
(1)、求证:△BED≌△BCD;(2)、若∠A=36°,求∠CFD的度数.25. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?