江苏省兴化市2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2020-12-23 类型:期中考试
一、单选题
-
1. - 2的相反数是( )A、- B、-2 C、 D、22. 下列各数中,属于无理数的是( )A、 B、3.1415926 C、2.010010001 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )A、2 B、5 C、4 D、35. 用代数式表示“x与y差的平方”,正确的是( )A、 B、 C、 D、6. 若代数式 的值是3,则代数式 的值是( )A、9 B、7 C、5 D、6
二、填空题
-
7. 某人身份证号码是321281198101208021,则他出生于月.8. 月球与地球的平均距离约为384000千米,将数384000用科学记数法表示为.9. 单项式 的次数为.10. 如图是一组数值转换机,若输入的 ,则输出的结果为.
 11. 一个两位数的十位数字是 ,个位上的数字是2,则这个两位数可表示成.(用含 的代数式表示).12. 绝对值小于3.6的所有负整数的和为.13. 若 是关于 的方程 的解,则 .14. 若 ,则 .15. 小明在某月历上圈出如图所示的呈十字形的5个数,如果圈出的五个数的和为65,那么其中最大的数为.
11. 一个两位数的十位数字是 ,个位上的数字是2,则这个两位数可表示成.(用含 的代数式表示).12. 绝对值小于3.6的所有负整数的和为.13. 若 是关于 的方程 的解,则 .14. 若 ,则 .15. 小明在某月历上圈出如图所示的呈十字形的5个数,如果圈出的五个数的和为65,那么其中最大的数为.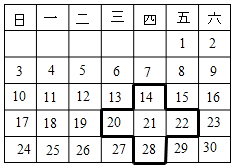 16. 已知: , ,无论 、 为何值,总有 ,则 .
16. 已知: , ,无论 、 为何值,总有 ,则 .三、解答题
-
17. 计算:(1)、(2)、(3)、(4)、18. 计算:(1)、(2)、19. 当 为何值时,代数式 的值与 的值互为相反数?20. 解下列方程:(1)、(2)、21. 先化简,再求值: [ ],其中a=-2.22. 网购的盛行,带动了快递行业的快速发展.一天快递员小李骑车从快递公司出发,在一条东西方向的马路上来回送件,规定在快递公司东边记为正,快递公司西边记为负,小李一天所走的路程记录如下:(单位:千米):+4,-3,+5,-2.5,2.5,-3,-2.8,+1.5,+1.5,-1.2.(1)、该快递员最后到达的地方在快递公司的哪个方向?距快递公司多远?(2)、该快递员在这次送件过程中,共走了多少千米?23. 已知 , .(1)、求 的值.(2)、当 , ,求 的值.24. 已知有理数a、b、c在数轴上的位置,
 (1)、a+b0;a+c0;b﹣c0用“>,<,=”填空)(2)、试化简|a+b|﹣|a+c|+|b﹣c|25. 用“*”定义一种新运算:对于任意有理数 和 ,规定 .如: .(1)、求 的值;(2)、若 ,求 的值;(3)、若 , (其中 为有理数),试比较 、 大小关系,并说明理由.26. 如图,数轴上点 表示数 ,点 表示数 ,数 、 满足 , 表示点 、 之间的距离,且 .
(1)、a+b0;a+c0;b﹣c0用“>,<,=”填空)(2)、试化简|a+b|﹣|a+c|+|b﹣c|25. 用“*”定义一种新运算:对于任意有理数 和 ,规定 .如: .(1)、求 的值;(2)、若 ,求 的值;(3)、若 , (其中 为有理数),试比较 、 大小关系,并说明理由.26. 如图,数轴上点 表示数 ,点 表示数 ,数 、 满足 , 表示点 、 之间的距离,且 . (1)、 , ;(2)、数轴上 点表示的数为 ,当 为何值时,点 到点 的距离等于点 到点 的距离的2倍?(3)、若在原点处放一挡板,一小球甲从点 处以3个单位长度/秒的速度向左运动,同时另一小球乙从点 处以4个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看为一点)立即以原来的速度向相反的方向运动,设运动的时间为 秒,求甲、乙两只小球到原点的距离相等时所对应的时间 (写出解答过程).
(1)、 , ;(2)、数轴上 点表示的数为 ,当 为何值时,点 到点 的距离等于点 到点 的距离的2倍?(3)、若在原点处放一挡板,一小球甲从点 处以3个单位长度/秒的速度向左运动,同时另一小球乙从点 处以4个单位长度/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看为一点)立即以原来的速度向相反的方向运动,设运动的时间为 秒,求甲、乙两只小球到原点的距离相等时所对应的时间 (写出解答过程).