江苏省东台市第五联盟2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2020-12-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各对数中互为相反数的是（）

A、 $- (+ 3)$ 和 $+ (- 3)$ B、 $+ (- 3)$ 和 $+ | - 3 |$ C、 $- (- 3)$ 和 $+ | - 3 |$ D、 $+ (- 3)$ 和 $- | + 3 |$

查看试题解析
2. 下列说法正确的是（）

A、 $- \frac{3 x y}{5}$ 系数是-3 B、x²+x-1的常数项为1 C、 $2^{2} a b^{3}$ 的次数是6次 D、2x-5x²+7是二次三项式

查看试题解析
3. 若x=2是关于x的方程2x+3m-1=0的解，则m的值为（）

A、-1 B、0 C、1 D、 $\frac{1}{3}$

查看试题解析
4. 下列各项中，去括号正确的是（）

A、x²－2(2x－y＋2)＝x²－4x－2y＋4 B、－3(m＋n)－mn＝－3m＋3n－mn C、－(5x－3y)＋4(2xy－y²)＝－5x＋3y＋8xy－4y² D、ab－5(－a＋3)＝ab＋5a－3

查看试题解析
5. 下面结论正确的有（）
①0是最小的整数；
②在数轴上7与9之间的有理数只有8；
③若a+b=0，则a、b互为相反数；
④有理数相减，差不一定小于被减数；
⑤1是绝对值最小的正数；
⑥有理数分为正有理数和负有理数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图所示，直线 $A B$ 、 $C D$ 相交于点 $O$ ，“阿基米德曲线”从点 $O$ 开始生成，如果将该曲线与每条射线的交点依次标记为2，－4，6，－8，10，－12，….那么标记为“－2020”的点在（）

A、射线 $O A$ 上 B、射线 $O B$ 上 C、射线 $O C$ 上 D、射线 $O D$ 上

查看试题解析
7. （-2）²⁰⁰⁴+3×（-2）²⁰⁰³的值为（）

A、-2²⁰⁰³ B、2²⁰⁰³ C、-2²⁰⁰⁴ D、2²⁰⁰⁴

查看试题解析
8. 如图，数轴上点M、N表示的数是m、n，点M在表示-3，-2的两点（包括这两点）之间移动，点N在表示-1，0的两点（包括这两点之间）移动，则以下对四个代数式的值判断正确的是（）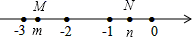

A、 $m^{2} - n$ 的值一定小于3 B、 $2 m + n$ 的值一定小于-7 C、 $\frac{1}{n - m}$ 值可能比2018大 D、 $\frac{1}{m} - \frac{1}{n}$ 的值可能比2018大

查看试题解析

二、填空题

9. 纪录片《厉害了，我的国》里介绍中国高速公路网于2018年达到13万1千公里，总里程世界第一，请你将13万1千公里用科学记数法表示为千公里.

查看试题解析
10. 若|x|=5，|y|=12，且x＞y，则x+y的值为．

查看试题解析
11. 一个三位数，十位数字为 $x$ ，个位数字比十位数字少3，百位数字是十位数字的3倍，则这个三位数为.

查看试题解析
12. 若 $a$ ， $b$ 互为相反数， $c$ ， $d$ 互为倒数， $m$ 的绝对值为 $2$ ，则 $\frac{a + b}{m} + m^{2} - c d$ 的值是.

查看试题解析
13. 淘宝“双十一”大促，某店铺一件标价为480的大衣打八折出售，仍可盈利20％，若设这件大衣的成本是x元，根据题意，可得到的方程是 .

查看试题解析
14. 若关于x、y的代数式mx³﹣3nxy²+2x³﹣xy²+y中不含三次项，则（m﹣3n）²⁰¹⁸=.

查看试题解析
15. 在一条可以折叠的数轴上，A，B表示的数分别是﹣9，4，如图，以点C为折点，将此数轴向右对折，若点A在点B的右边，且AB＝1，则C点表示的数是.

查看试题解析
16. 一列方程如下排列：
$\frac{x}{4} + \frac{x - 1}{2} = 1$ 的解是 $x = 2$ ，

$\frac{x}{6} + \frac{x - 2}{2} = 1$ 的解是 $x = 3$ ，

$\frac{x}{8} + \frac{x - 3}{2} = 1$ 的解是 $x = 4$ ，

……

根据观察得到的规律，写出其中解是 $x = 2020$ 的方程。

查看试题解析

三、解答题

17. 将 $2$ ， $- \frac{3}{2}$ ， $0$ ， $5.34$ ， $\frac{1}{2}$ ， $π$ ， ${(- 2)}^{2}$ ， $- (- 3)$ ， $- 2^{2}$ 的整数在数轴上表示出来.

查看试题解析
18. 计算：

(1)、 $54 \times (\frac{5}{6} - \frac{4}{9} + \frac{1}{3})$ ；

(2)、 $- 1^{2016} - (1 - 0.5) \times \frac{1}{3} \times [2 - {(- 3)}^{2}]$

查看试题解析
19. 解方程：

(1)、2x+3=x－1

(2)、 $\frac{x - 3}{0.15} - \frac{x + 4}{0.2}$ =﹣10

查看试题解析
20. 若单项式 $3 x^{2} y^{5} 与 - 2 x^{1 - a} y^{3 b - 1}$ 是同类项，求下面代数式的值： $5 {ab}^{2} - [6 a^{2} b - 3 (a b^{2} + 2 a^{2} b)]$

查看试题解析
21. 某同学在计算 $2 x^{2} - 5 x + 6$ 减去某个多项式时，由于粗心，误算为加上这个多项式，而得到 $4 x^{2} - 4 x + 6$ ，请求出正确的答案.

查看试题解析
22. 已知A= $2 x^{2} + x y + 3 y$ ，B= $x^{2} - x y$ .若 ${(x + 2)}^{2} + | y - 3 | = 0$ ；

(1)、求 $x, y$ 的值.

(2)、求A-2B的值，

查看试题解析
23. 有理数 $a$ 、 $b$ 、 $c$ 在数轴上的位置如图：

(1)、判断正负，用“>”或“<”填空： $b$ －c0， $a$ ＋ $b$ 0，c－ $a$ 0.

(2)、化简：|b－c|＋| $a$ ＋b|－|c－a|

查看试题解析
24. 有一条长度为 a 的线段.

(1)、如图①，以该线段为直径画一个圆，该圆的周长 C1 = ；如图②，分别以该线段的一半为直径画两个圆，这两个圆的周长的和 C2 = （都用含 a 的代数式表示，结果保留p ）

(2)、如图③，在该线段上任取一点，再分别以两条小线段为直径画两个圆，这两个圆的周长的和为 C3 ，探索 C1 和 C3 的数量关系，并说明理由。

(3)、如图④，当 a =10 时，以该线段为直径画一个大圆，再在大圆内画若干个小圆，这些小圆的直径都和大圆的直径在同一条直线上，且小圆的直径的和等于大圆的直径，那么图中所有圆的周长的和为（结果保留p ）

查看试题解析
25. 在数学问题中，我们常用几何方法解决代数问题，借助数形结合的方法使复杂问题简单化.
材料一：我们知道|a|的几何意义是：数轴上表示数a的点到原点的距离；|a﹣b|的几何意义是：数轴上表示数a，b的两点之间的距离；|a+b|的几何意义是：数轴上表示数a，﹣b的两点之间的距离；根据绝对值的几何意义，我们可以求出以下方程的解.

（ 1 ）|x﹣3|＝4

解：由绝对值的几何意义知：

在数轴上x表示的点到3的距离等于4

∴x₁＝3+4＝7，x₂＝3﹣4＝﹣1

（ 2 ）|x+2|＝5

解：∵|x+2|＝|x﹣（﹣2）|，∴其绝对值的几何意义为：在数轴上x表示的点到﹣2的距离等于5.∴x₁＝﹣2+5＝3，x₂＝﹣2﹣5＝﹣7

材料二：如何求|x﹣1|+|x+2|的最小值.

由|x﹣1|+|x+2|的几何意义是数轴上表示数x的点到表示数1和﹣2两点的距离的和，要使和最小，则表示数x的这点必在﹣2和1之间（包括这两个端点）取值.

∴|x﹣1|+|x+2|的最小值是3；由此可求解方程|x﹣1|+|x+2|＝4，把数轴上表示x的点记为点P，由绝对值的几何意义知：当﹣2≤x≤1时，|x﹣1|+|x+2|恒有最小值3，所以要使|x﹣1|+|x+2|＝4成立，则点P必在﹣2的左边或1的右边，且到表示数﹣2或1的点的距离均为0.5个单位.

故方程|x﹣1|+|x+2|＝4的解为：x₁＝﹣2﹣0.5＝﹣2.5，x₂＝1+0.5＝1.5.

阅读以上材料，解决以下问题：

(1)、填空：|x﹣3|+|x+2|的最小值为；

(2)、已知有理数x满足：|x+3|+|x﹣10|＝15，有理数y使得|y﹣3|+|y+2|+|y﹣5|的值最小，求x﹣y的值.

(3)、试找到符合条件的x，使|x﹣1|+|x﹣2|+…+|x﹣n|的值最小，并求出此时的最小值及x的取值范围.

查看试题解析