江苏省苏州市吴中、吴江区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-23 类型:期中考试
一、单选题
-
1. 下列方程中,属于一元二次方程的是( )A、x+1=0 B、x2=2x﹣1 C、2y﹣x=1 D、x2+3=2. 方程x2=3x的解为( )A、x=3 B、x=0 C、x1=0,x2=﹣3 D、x1=0,x2=33. 如图,点 、 、 在 上,若 ,则 的度数是( )
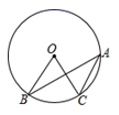 A、18° B、36° C、54° D、72°4. 九年级(1)班甲、乙、丙、丁四名同学几次数学测试成绩的平均数 (分)及方差S2如下表:
A、18° B、36° C、54° D、72°4. 九年级(1)班甲、乙、丙、丁四名同学几次数学测试成绩的平均数 (分)及方差S2如下表:甲
乙
丙
丁
平均数(分)
95
97
95
97
方差
0.5
0.5
0.2
0.2
老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选( )
A、甲 B、乙 C、丙 D、丁5. 一元二次方程x2+kx﹣3=0的一个根是x=1,则k的值为( )A、2 B、﹣2 C、3 D、﹣36. 已知圆锥的底面半径为3cm,母线长为6cm,则圆锥的侧面积是( )A、18cm2 B、 C、27cm2 D、7. 如图,在边长为4的正方形 中,以点 为圆心, 为半径画弧,交对角线 于点 ,则图中阴影部分的面积是(结果保留 )( ) A、 B、 C、 D、8. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心( ).
A、 B、 C、 D、8. 10个大小相同的正六边形按如图所示方式紧密排列在同一平面内,A,B,C,D,E,O均是正六边形的顶点.则点O是下列哪个三角形的外心( ). A、 B、 C、 D、9. 根据下列表格的对应值:
A、 B、 C、 D、9. 根据下列表格的对应值:x
0.59
0.60
0.61
0.62
0.63
x2+x-1
-0.0619
-0.04
-0.0179
0.0044
0.0269
判断方程x2+x-1=0一个解的取值范围是( )
A、0.59<x<0.60 B、0.60<x<0.61 C、0.61<x<0.62 D、0.62<x<0.6310. 如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切菱形的顶点A到圆心O的距离为5,则⊙O的半径长等于( )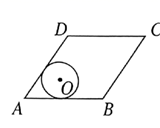 A、2.5 B、 C、 D、3
A、2.5 B、 C、 D、3二、填空题
-
11. 方程x2=9的解为12. 若⊙O的半径为3,点P为平面内一点,OP=2,那么点P在⊙O(填“上”、“内部”或“外部”)13. 一组数据4,1,7,4,5,6则这组数据的极差为.14. 三角形两边的长分别是3和4,第三边的长是方程 的根,则该三角形的周长为.15. 已知关于 的一元二次方程 有两个不相等的实数根,则实数 的取值范围是.16. 如图,△ABC内接于⊙O,∠BAC=30°,BC=2,则⊙O的直径等于.
 17. 如图,AB是⊙O的直径,AB=20cm,弦BC=12cm,F是弦BC的中点.若动点E以2cm/s的速度从A点出发沿着AB方向运动,设运动时间为t(s)(0≤t≤10),连接EF,当△BEF是直角三角形时,t(s)的值为.
17. 如图,AB是⊙O的直径,AB=20cm,弦BC=12cm,F是弦BC的中点.若动点E以2cm/s的速度从A点出发沿着AB方向运动,设运动时间为t(s)(0≤t≤10),连接EF,当△BEF是直角三角形时,t(s)的值为.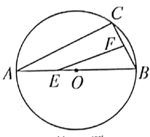 18. 我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.在平面直角坐标系xOy中,图形G为以原点O为圆心,2为半径的圆,则点A(1,-1)到图形G的距离跨度是.
18. 我们规定:平面内点A到图形G上各个点的距离的最小值称为该点到这个图形的最小距离d,点A到图形G上各个点的距离的最大值称为该点到这个图形的最大距离D,定义点A到图形G的距离跨度为R=D-d.在平面直角坐标系xOy中,图形G为以原点O为圆心,2为半径的圆,则点A(1,-1)到图形G的距离跨度是.三、解答题
-
19. 解方程:(1)、(2)、20.(1)、根据要求,解答下列问题:
①方程 的解为;
②方程 的解为;
③方程 的解为;
(2)、根据以上方程特征及其解的特征,请猜想:①方程 的解为.
②关于x的方程的解为x1=1,x2=n;
(3)、请用配方法解方程 ,以验证猜想结论的正确性.21. 为了了解某校八年级学生每周平均课外阅读时间的情况,随机抽取了50名八年级学生,对其每周平均课外阅读时间进行统计,并绘制成下面的统计图。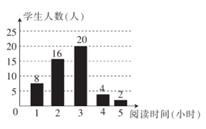 (1)、这50名同学每周阅读时间的众数为小时,中位数为小时。(2)、求出这组数据的平均数。22. “疫情”期间,某小区准备搭建一个面积为12平方米的矩形临时隔离点ABCD,如图所示,矩形一边利用一段已有的围墙(可利用的围墙长度仅有5米),另外三边用9米长的建筑材料围成,为方便进出,在与围墙平行的一边要开一扇宽度为1米的小门EF,求AB的长度为多少米?
(1)、这50名同学每周阅读时间的众数为小时,中位数为小时。(2)、求出这组数据的平均数。22. “疫情”期间,某小区准备搭建一个面积为12平方米的矩形临时隔离点ABCD,如图所示,矩形一边利用一段已有的围墙(可利用的围墙长度仅有5米),另外三边用9米长的建筑材料围成,为方便进出,在与围墙平行的一边要开一扇宽度为1米的小门EF,求AB的长度为多少米? 23. 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OA、OD、OE、AE、DE.
23. 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在弧AD上,连接OA、OD、OE、AE、DE.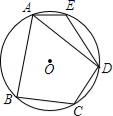 (1)、求∠AED的度数;(2)、当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.24. 已知关于x的一元二次方程(1)、求证:不论m为何值,该方程总有两个实数根;(2)、若x=1是该方程的根,求代数式 的值.25. “疫情”期间,李晨在家制作一种工艺品,并通过网络平台进行线上销售.经过一段时间后发现:当售价是40元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出3件,设该商品的售价为x元/件(20≤x≤40).(1)、请用含售价x(元/件)的代数式表示每天能售出该工艺品的件数;(2)、已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为900元.
(1)、求∠AED的度数;(2)、当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.24. 已知关于x的一元二次方程(1)、求证:不论m为何值,该方程总有两个实数根;(2)、若x=1是该方程的根,求代数式 的值.25. “疫情”期间,李晨在家制作一种工艺品,并通过网络平台进行线上销售.经过一段时间后发现:当售价是40元/件时,每天可售出该商品60件,且售价每降低1元,就会多售出3件,设该商品的售价为x元/件(20≤x≤40).(1)、请用含售价x(元/件)的代数式表示每天能售出该工艺品的件数;(2)、已知每件工艺品需要20元成本,每天销售该工艺品的纯利润为900元.①求该商品的售价;
②为了支持“抗疫”行动,李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元,求李晨每天通过销售该工艺品捐款的数额.
26. 如图,在Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB,连接DO并延长交CB的延长线于点E.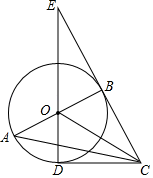 (1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=2,DE=4,求圆的半径及AC的长.27. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.
(1)、判断直线CD与⊙O的位置关系,并说明理由;(2)、若BE=2,DE=4,求圆的半径及AC的长.27. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.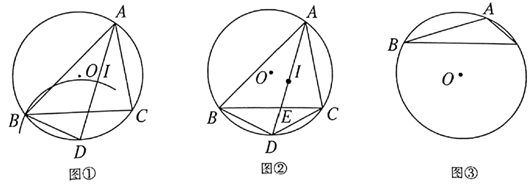 (1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证: ;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.28. 如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动,设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示:
(1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证: ;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.28. 如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB→BC→CD向点D运动,设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所示: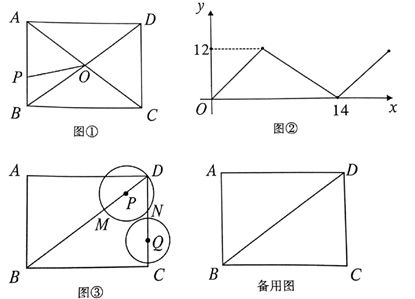 (1)、AD边的长为.(2)、如图③,动点P到达点D后从D点出发,沿着DB方向以1个单位长度/秒的速度匀速运动,以点P为圆心,PD长为半径的⊙P与DB、DC的另一个交点分别为M、N,与此同时,点Q从点C出发,沿着CD方向也以1个单位长度/秒的速度匀速运动,以点Q为圆心、2为半径作⊙Q.设运动时间为t秒(0<t≤5).
(1)、AD边的长为.(2)、如图③,动点P到达点D后从D点出发,沿着DB方向以1个单位长度/秒的速度匀速运动,以点P为圆心,PD长为半径的⊙P与DB、DC的另一个交点分别为M、N,与此同时,点Q从点C出发,沿着CD方向也以1个单位长度/秒的速度匀速运动,以点Q为圆心、2为半径作⊙Q.设运动时间为t秒(0<t≤5).①当t为何值时,点Q与点N重合?
②当⊙P与BC相切时,求点Q到BD的距离.